2015-07-21
483
Примером фильтра второго порядка является фильтр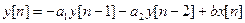 
.
Рассматриваем только вещественный случай. Переходя к Z - преобразованию, получим:
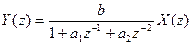. (5.6.9)
Найдя корни многочлена в знаменателе, перепишем
|
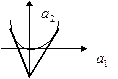
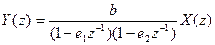. Это означает, что фильтр есть последовательное соединение двух фильтров первого порядка. Для устойчивости достаточно потребовать, чтобы все корни были по модулю меньше единицы. Это означает, что 
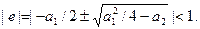. Рассмотрим вещественный случай: 
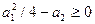. Это область под параболой. Условие на модуль первого корня имеет вид 
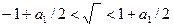. Возводя второе неравенство в квадрат, получим 
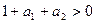. Для выполнения первого из неравенств достаточно чтобы 
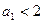. Аналогичное рассмотрение условия на второй корень дает 
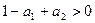. Окончательно, область имеет форму. Для комплексных корней 
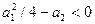. Кроме того, квадрат модуля корня равен 
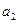, откуда вытекает, что 
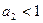. Объединяя обе области, получаем треугольник устойчивости.
Другими словами, если точка с координатами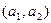 
попадает внутрь треугольника, соответствующий фильтр будет устойчивым.
