Требуется найти значение определенного интеграла 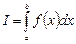 для некоторой заданной на отрезке
для некоторой заданной на отрезке 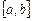 функции
функции 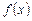 . Для некоторых функций значение интеграла можно найти точно. Однако в общем случае значение интеграла можно найти только приближенно, используя тот или иной способ численного интегрирования.
. Для некоторых функций значение интеграла можно найти точно. Однако в общем случае значение интеграла можно найти только приближенно, используя тот или иной способ численного интегрирования.
Численное интегрирование основано на замене интеграла некой суммой 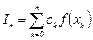 . Такая замена следует из определения интеграла как предела суммы
. Такая замена следует из определения интеграла как предела суммы 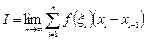 . Зафиксировав
. Зафиксировав 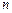 , мы получим предыдущую сумму.
, мы получим предыдущую сумму.
Приближенное равенство 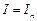 называется квадратурной формулой,
называется квадратурной формулой, 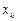 – узлами, а
– узлами, а 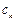 - коэффициентами квадратурной формулы. Разность
- коэффициентами квадратурной формулы. Разность 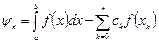 называется погрешностью квадратурной формулы.
называется погрешностью квадратурной формулы.
Разобьем отрезок 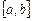 на
на 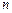 равных частей точками
равных частей точками 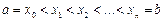 . Получим равномерную сетку:
. Получим равномерную сетку: 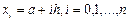 . Тогда
. Тогда 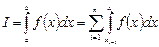 .
.
Для построения квадратурной формулы на всем отрезке 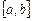 достаточно построить квадратурную формулу на частичном отрезке
достаточно построить квадратурную формулу на частичном отрезке 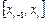 .
.
 2015-07-21
2015-07-21 305
305








