Глобальная интерполяция

В случае глобальной интерполяции отыскивается единая интерполирующая функция на всем интервале 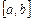. Самым распространенным способом является полиномиальная интерполяция.

Будем искать интерполирующую функцию в виде полинома (многочлена) 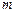-ой степени 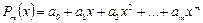. Какова должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции? Допустим, что заданы две точк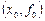и: и 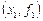, т.е. 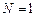. Через эти точки можно провести единственную прямую, т.е. интерполирующей функцией будет полином первой степени 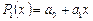. Через три точки (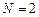) можно провести параболу 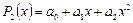и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень .

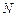Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции при каждом :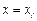

.

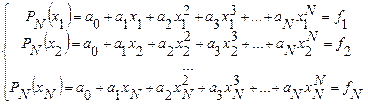
Данная система является линейной относительно искомых коэффициентов 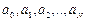_. Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля. Определитель данной системы

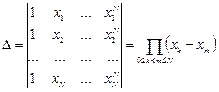
носит имя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если 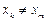. В нашем случае это означает, что все узлы интерполяции различны, что верно по определению. Таким образом, доказано, что система имеет решение.

Мы показали, что для нахождения коэффициентов 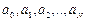надо решить СЛАУ, что является сложной задачей. Но есть другой способ построения полинома 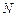-й степени, который не требует решения такой системы.