Решение ищем в виде 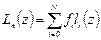 , где
, где 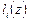 – базисные полиномы
– базисные полиномы 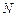 -й степени, для которых выполняется условие:
-й степени, для которых выполняется условие: 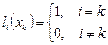 . Убедимся в том, что если такие полиномы построены, то
. Убедимся в том, что если такие полиномы построены, то 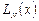 будет удовлетворять условиям интерполяции:
будет удовлетворять условиям интерполяции: 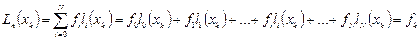 Каким образом построить базисные полиномы? Определим
Каким образом построить базисные полиномы? Определим
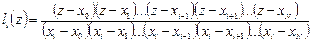 ,
, 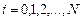 .
.
Легко понять, что
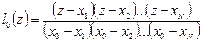 ,
, 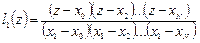 , и т.д.
, и т.д.
Функция 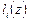 является полиномом
является полиномом 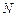 –й степени от
–й степени от 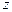 и для нее выполняются условия «базисности»:
и для нее выполняются условия «базисности»:
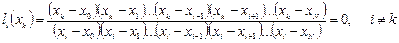 , т.е.
, т.е. 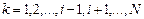 ;
;
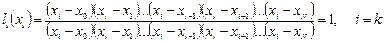 .
.
Таким образом, нам удалось решить задачу о построении интерполирующего полинома 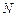 -й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы:
-й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы: 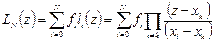 . Погрешность этой формулы можно оценить, если исходная функция
. Погрешность этой формулы можно оценить, если исходная функция 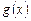 имеет производные до
имеет производные до 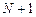 порядка:
порядка:
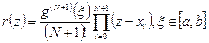 .
.
Из этой формулы следует, что погрешность метода зависит от свойств функции 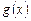 , а также от расположения узлов интерполяции и точки
, а также от расположения узлов интерполяции и точки 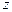 . Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях
. Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях 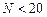 . При бόльших
. При бόльших 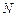 погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом
погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом 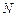 ).
).
Рассмотрим частные случаи. Пусть 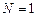 , т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:
, т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:
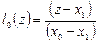 ,
, 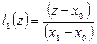 ,
, 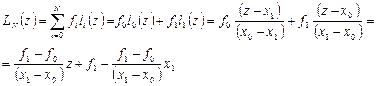 ,
,
т.е. получаем формулы кусочно-линейной интерполяции.
Пусть 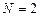 . Тогда:
. Тогда:
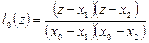 ,
, 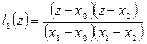 ,
, 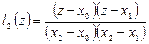 ,
,
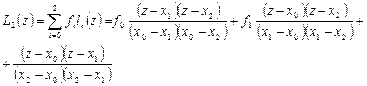 .
.
В результате мы получили формулы, так называемой квадратичной или параболической интерполяции.
ПРИМЕР 3.3. Задана таблица значений функции:
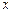
| 3,5 | |||
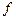
| -1 | 0,2 | 0,5 | 0,8 |
Требуется найти значение функции при 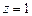 , используя интерполяционный полином Лагранжа. Для этого случая
, используя интерполяционный полином Лагранжа. Для этого случая 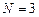 , т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при
, т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при 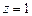 :
:
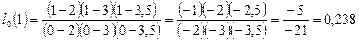 ,
,
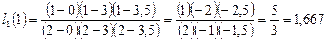 ,
,
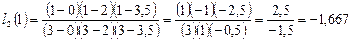 ,
,
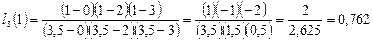
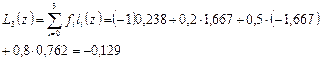
Итак, интерполирующая функция принимает в точке 1 значение -0,129.
 2015-07-21
2015-07-21 713
713








