При вычислении интеграла 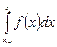 с помощью метода Симпсона (парабол), функцию
с помощью метода Симпсона (парабол), функцию 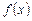 на локальном отрезке
на локальном отрезке 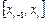 заменяют параболой, проходящей через точки
заменяют параболой, проходящей через точки 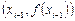 ,
, 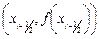 ,
, 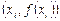 , где
, где 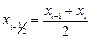 – середина локального отрезка. Построим полином Лагранжа второй степени:
– середина локального отрезка. Построим полином Лагранжа второй степени:
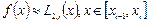
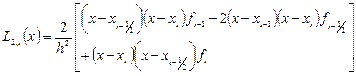 .
.
Здесь 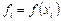 ,
, 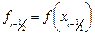 ,
, 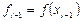 .
.
Тогда
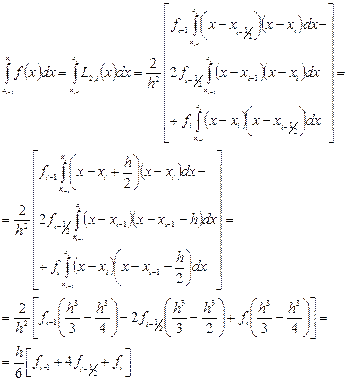
Таким образом, мы получаем формулу Симпсона
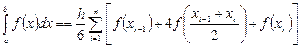 .
.
Можно показать, что формула Симпсона имеет четвертый порядок точности.
ПРИМЕР 4.1. Вычислить интеграл J = 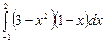 .
.
Найдем значение определенного интеграла точно:
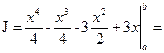 5,25.
5,25.
Разобьем отрезок 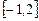 на 10 частей, т.е.
на 10 частей, т.е.  . Вычислим значение интеграла по формулам левых, правых, средних прямоугольников, по формуле трапеций и формуле Симпсона. Для этого составим таблицы:
. Вычислим значение интеграла по формулам левых, правых, средних прямоугольников, по формуле трапеций и формуле Симпсона. Для этого составим таблицы:
| 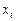
| 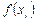
| 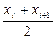
| 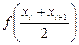
| 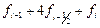
|
| -1 | -0.85 | 4.213375 | 25.1205 | ||
| -0.7 | 4.267 | -0.55 | 4.181125 | 24.9675 | |
| -0.4 | 3.976 | -0.25 | 3.671875 | 21.9525 | |
| -0.1 | 3.289 | 0.05 | 2.847625 | 17.0475 | |
| 0.2 | 2.368 | 0.35 | 1.870375 | 11.2245 | |
| 0.5 | 1.375 | 0.65 | 0.902125 | 5.4555 | |
| 0.8 | 0.472 | 0.95 | 0.104875 | 0.7125 | |
| 1.1 | -0.179 | 1.25 | -0.35938 | -2.0325 | |
| 1.4 | -0.416 | 1.55 | -0.32863 | -1.8075 | |
| 1.7 | -0.077 | 1.85 | 0.359125 | 2.3595 | |
Для нахождения интеграла методом левых прямоугольников, необходимо просуммировать элементы третьего ряда в диапазоне  и умножить на шаг
и умножить на шаг 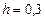 . Аналогично для формулы правых прямоугольников, суммировать в диапазоне
. Аналогично для формулы правых прямоугольников, суммировать в диапазоне 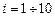 . Сумма элементов пятого столбца, помноженная на шаг, даст результат по формуле средних прямоугольников. Согласно формуле трапеций, необходимо к полусумме первого и последнего значения элементов третьего столбца добавить сумму всех остальных членов этого столбца, и умножить результат на шаг
. Сумма элементов пятого столбца, помноженная на шаг, даст результат по формуле средних прямоугольников. Согласно формуле трапеций, необходимо к полусумме первого и последнего значения элементов третьего столбца добавить сумму всех остальных членов этого столбца, и умножить результат на шаг 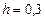 . Суммируя значения последнего столбца и умножая ее на
. Суммируя значения последнего столбца и умножая ее на 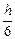 =0,05, найдем интеграл по методу Симпсона, результаты соберем в таблицу:
=0,05, найдем интеграл по методу Симпсона, результаты соберем в таблицу:
| Формула левых прямоугольников | 5.7225 |
| Формула правых прямоугольников | 4.8225 |
| Формула средних прямоугольников | 5.23875 |
| Формула трапеций | 5.2725 |
| Формула Симпсона | 5.25 |
Как следует из таблицы, для данной подынтегральной функции формула левых прямоугольников дает приближенное значение с избытком, а формула правых прямоугольников – с недостатком. Хорошую точность дали метод трапеций и метод средних прямоугольников. Результаты различаются, поскольку значения известной подынтегральной функции в методе средних были вычислены в средних точках, а не получены путем интерполяции. Метод Симпсона дал абсолютно точное значение интеграла. Это связано с тем, что первообразная функция в данном примере является полиномом четвертого порядка, для которых метод Симпсона дает точное значение.
 2015-07-21
2015-07-21 472
472








