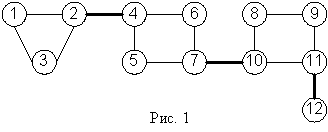
Определение. Мостом (рис. 1) называют такое ребро 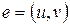 графа
графа 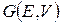 , что его удаление из графа увеличивает на единицу число компонент связности. Другими словами, вершины и и v перестают быть связными. На рис.1 мосты – это ребра (2, 4), (7, 10), (11, 12).
, что его удаление из графа увеличивает на единицу число компонент связности. Другими словами, вершины и и v перестают быть связными. На рис.1 мосты – это ребра (2, 4), (7, 10), (11, 12).
Теорема о свойствах мостов.
Пусть G = (V,E)связный граф, 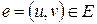 – ребро данного графа. Тогда следующие утверждения эквивалентны
– ребро данного графа. Тогда следующие утверждения эквивалентны
1. е – мост.
2. е не принадлежит никакому простому циклу.
3. е – единственная простая цепь, соединяющая вершины и и v.
4. Множество вершин V можно разбить на два пересекающихся подмножества V 1 и V 2так, что 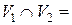 Æ,
Æ, 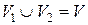 ,
, 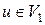 ,
, 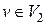 и всякая простая цепь, соединяющая любую вершину
и всякая простая цепь, соединяющая любую вершину 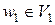 c любой вершиной
c любой вершиной 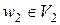 , проходит через ребро е.
, проходит через ребро е.
Доказательство.
1 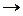 2. Дано:
2. Дано: 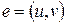 – мост.
– мост.
Доказать: Ребро е не принадлежит никакому простому циклу.
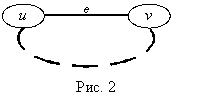
Пусть е принадлежит циклу (рис. 2), но тогда его удаление не нарушит связности вершин u и v – противоречие.
2 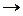 3. Дано: ребро е не принадлежит никакому простому циклу.
3. Дано: ребро е не принадлежит никакому простому циклу.
Доказать: е – единственная простая цепь, соединяющая вершины и и v.
Допустим, что существует другая простая цепь, соединяющая вершины и и v. Если объединить ее с ребром е, получится цикл, проходящий через ребро е, – противоречие.
3 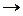 4. Дано: е – единственная простая цепь, соединяющая вершины и и v.
4. Дано: е – единственная простая цепь, соединяющая вершины и и v.
Доказать: Множество V вершин можно разбить на два пересекающихся подмножества в соответствии с условием 4.
Удалим из графа ребро е – единственную простую цепь, соединяющую вершины и и v. Связь между вершинами будет разорвана, они окажутся лежащими в разных компонентах связности. Обозначим их 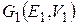 (и
(и 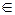 V 1) и
V 1) и 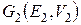 (v
(v 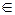 V 2). Тогда
V 2). Тогда 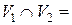 Æ,
Æ, 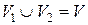 .
.
Пусть 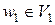 ,
, 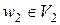 . Так как исходный граф G был связен, в нем существовали простые цепи, соединяющие вершины
. Так как исходный граф G был связен, в нем существовали простые цепи, соединяющие вершины 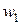 и
и 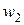 . Все они исчезли после удаления е. Значит, все они через ребро е проходили.
. Все они исчезли после удаления е. Значит, все они через ребро е проходили.
4 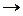 1. Дано: Выполняется утверждение 4.
1. Дано: Выполняется утверждение 4.
Доказать: 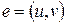 – мост.
– мост.
Так как 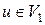 и
и 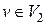 , то любая простая цепь, соединяющая вершины и и v, проходит через ребро е, значит, его удаление разрывает связь между этими вершинами.
, то любая простая цепь, соединяющая вершины и и v, проходит через ребро е, значит, его удаление разрывает связь между этими вершинами.
 2015-07-21
2015-07-21 1120
1120







