Пусть 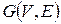 – связный граф.
– связный граф.
Определение. Остовным деревом связного графа 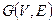 называют всякий его остовный подграф, который является деревом.
называют всякий его остовный подграф, который является деревом.
Если в графе 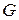 всего р вершин, то в остовном дереве
всего р вершин, то в остовном дереве 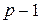 ребер. Чтобы построить остовное дерево графа, нужно последовательно удалять ребра, принадлежащие циклам, пока все циклы не будут разрушены. Если в графе
ребер. Чтобы построить остовное дерево графа, нужно последовательно удалять ребра, принадлежащие циклам, пока все циклы не будут разрушены. Если в графе 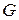 всего q ребер, то, чтобы получить остовное дерево, потребуется удалить
всего q ребер, то, чтобы получить остовное дерево, потребуется удалить 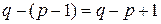 ребро.
ребро.
На рис. 10 показаны два различных остовных дерева (Т 1 и Т 2) исходного графа 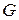 .
.

 2015-07-21
2015-07-21 1758
1758








