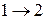Доказательство

. Рассмотрим граф 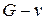. Так как v – точка сочленения, то граф 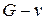не связен, так что число k его компонент связности 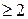. Выберем произвольно две компоненты связности графа 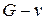: 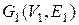и 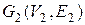. Пусть 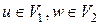. В графе 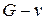не существует простой цепи, соединяющей вершины u и w. Но в исходном графе G такие цепи были, ведь граф G был связен. Все они исчезли после удаления вершины v, значит, все они через неё проходили.

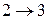. Допустим, что вершина v – это висячая вершина некоторого остовного дерева T графа G (рис. 2)

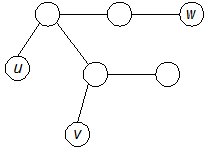
Рис. 2

Тогда две любые другие вершины u и w дерева T, отличные от вершины v, соединены в T (и, значит, в G) простой цепью, не проходящей через вершину v – противоречие.

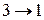. Легко видеть, что во всяком дереве висячие вершины и только они не являются точками сочленения.

Если v – не есть висячая вершина никакого остовного дерева графа G, её удаление разрушит все остовные деревья этого графа. Что и означает разделение связного графа на несколько компонент связности.

Следствие. Так как во всяком дереве есть по крайней мере две висячие вершины, то во всяком графе по крайней мере две вершины не являются точками сочленения.