2015-07-14
1436
Соотношения (7) и (15) дают мощное эвристическое средство для квантовых оценок характерных масштабов и значений энергий микроскопических физических систем. Рассмотрим два примера применения этого принципа.
Задача 4. Допустим, к примеру, мы решили удерживать частицу массы m в области размером b. Для этого по обе стороны частицы поставили две жесткие пластинки и стали очень медленно сближать их. Задача состоит в том, чтобы выяснить, какова будет реакция частицы на эту процедуру.
Решение. Положение частицы имеет неопределенность Dx=b. Частица в этих условиях не может находиться в покое. Ее импульс будет иметь неопределенность
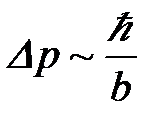. (16)
А так как в среднем частица остается на месте, такие же характерные значения имеет и импульс частицы. Таким образом, следует ожидать, что характерные значения кинетической энергии частицы E=p2/2m будут такими:
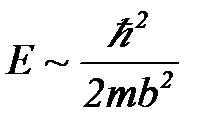(17)
- при уменьшении расстояния между пластинками энергия частицы увеличивается. То есть, чтобы сблизить пластинки надо совершить работу. Из этого следует, что частица создает давление на пластинки. Чтобы локализовать распределение амплитуд вероятности частицы в области бесконечно малых размеров, надо совершить бесконечно большую работу.
Проведенный анализ показывает, что распределение амплитуд вероятности частицы обладает упругостью, как какая-нибудь упругая среда. Это налагает определенные ограничения на поведение и на возможные конфигурации распределений. В частности изменение распределения амплитуд в пространстве должно быть плавным, без резких скачков и разрывов.
Из (17) так же следует, что тяжелую частицу локализовать в малой области пространства легче, чем частицу меньшей массы. По этой причине мюоноводород (водород, в котором роль электрона играет мюон, который в 207 раз тяжелее электрона) имеет размеры гораздо меньшие, чем настоящий водород.
Задача 4. Используя соотношение неопределенностей импульса и координаты оценить энергию основного состояния атома водорода и его размер.
Решение. Так как масса электрона много меньше массы протона, будем считать, что движется только электрон, а протон покоится. В основу расчетов возьмем положение о том, что система, предоставленная сама себе, оказывается в состоянии с наименьшей энергией. Полная энергия электрона равна сумме кинетической и потенциальной энергий:
E=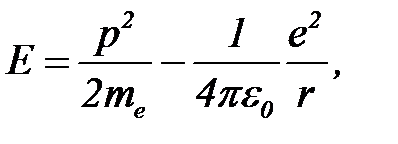 
(18)
где r - расстояние между электроном и протоном. Так как в связанном состоянии электрон не улетает далеко от протона, можно считать, что это расстояние равно размеру области локализации электрона, т.е. неопределенности координаты. В таком случае импульс электрона имеет неопределенность
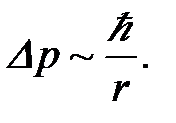(19)
А так как в среднем частица остается на месте, такие же характерные значения имеет и сам импульс частицы. Таким образом, следует ожидать, что характерные значения полной энергии частицы должны удовлетворять соотношению:
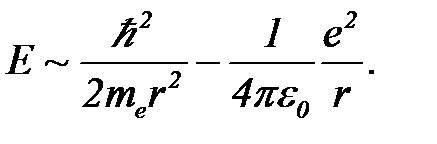(20)
При уменьшении размера r потенциальная энергия убывает пропорционально - 1/r, а кинетическая энергия возрастает пропорционально 1/r2. Значит, должно существовать оптимальное значение r, при котором полная энергия принимает наименьшее значение. Оно определится из условия минимума:
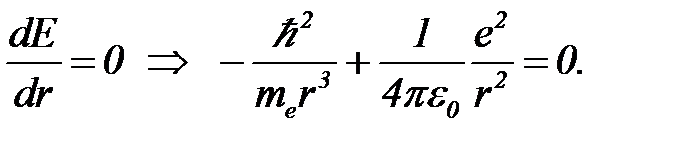(21)
Из уравнения (21) находим оптимальный размер области локализации электрона
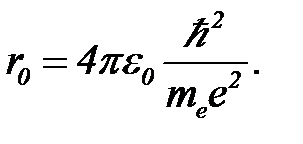(22)
Нетрудно увидеть, что это выражение точно совпадает с выражением первого боровского радиуса. Подстановка значений констант дает r0=
=0,53×10-10м.
После подстановки выражения (22) в формулу (20), находим
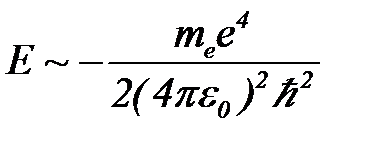. (23)
Разумеется, это оценка по порядку величины.Но случайно оказалось, что данное значение прекрасно согласуется с экспериментальными данными по ионизации атома водорода: E»13,6 эВ.
