Способы формирования зоны обнаружения

Для успешного решения задач радиолокационной разведки и выдачи информации зона обнаружения РЛС (РЛК) боевого режима в вертикальной плоскости должна быть косекансной (см. рис. 2.1). Её основными параметрами являются максимальная дальность 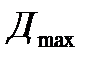, высота 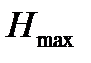обнаружения целей с определенной ЭПР, минимальный 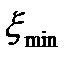и максимальный 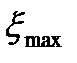углы места. Иногда в качестве параметра используют также угол места 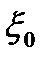, при котором определяется переход от изодальностного участка зоны к изовысотному.

Проведем анализ уравнения радиолокации для изодальностного участка зоны обнаружения (см. рис. 2.1). Будем полагать, что в процессе обзора зоны обнаружения антенный луч приемной антенны не изменяет своей ширины (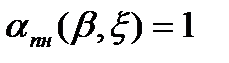 при 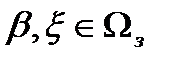). В случае изодальностной зоны

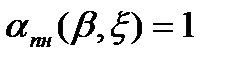при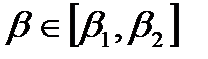

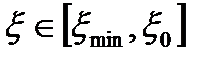
где 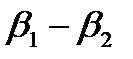- угловой размер зоны обнаружения в азимутальной плоскости (в радиолокационных дальномерах он равен 360).Интеграл в знаменателе уравнения (2.12)

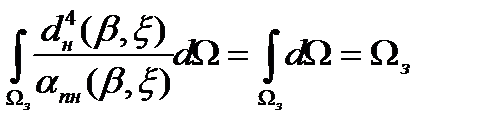
Выразим телесный угол изодальностной зоны обнаружения 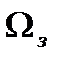через угловые размеры зоны в азимутальной и угломестной плоскостях. С учетом соотношения (2.1) получим

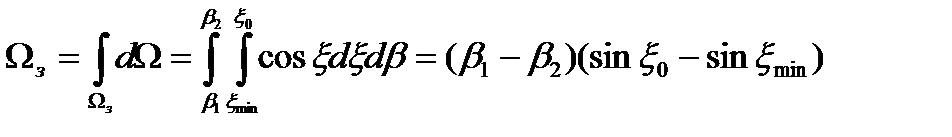
Подставим значение 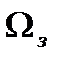в исходное уравнение (2.12) и получим

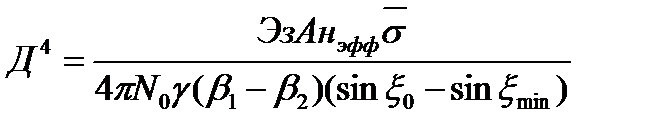(2.14)

СТР 16

---------------------------------------------------------------------------------------------------------------------

Дальность до точек граничной поверхности для изовысотной части зоны обнаружения (рис. 2.1) Определяется выражением

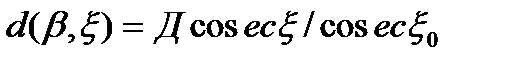при 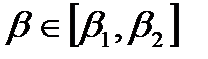(2.15)

Рассмотрим два способа формирования изовысотного участка зоны обнаружения.

1) В процессе обзора зоны обнаружения главный лепесток ДН приемной антенны не изменяет своей ширины т.е. 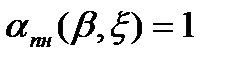в пределах углов 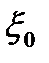… 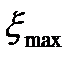. Требуемая форма зоны обнаружения в этом случае может формироваться за счет изменения в угломестной плоскости величины излучаемой средней мощности или коэффициента усиления передающей антенны по закону

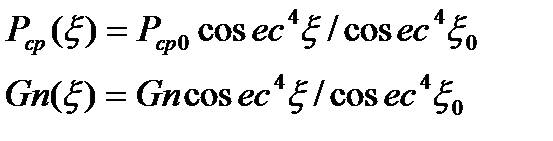
С выражения (2.15) получим

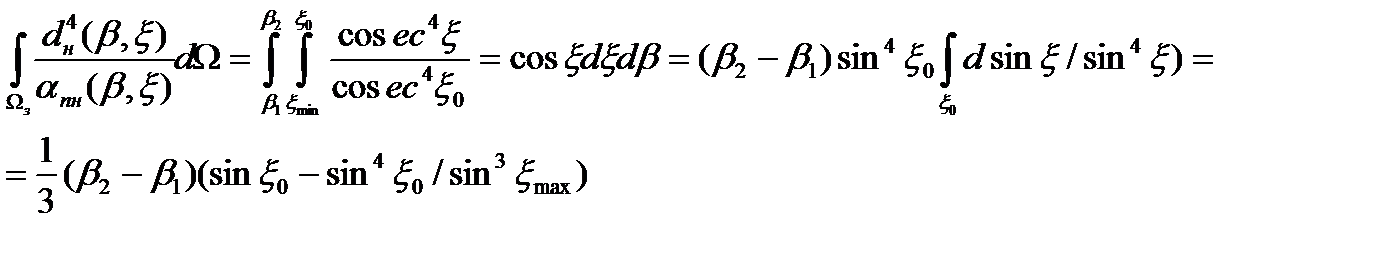(2.16)

При вычислении формулы (2.16) учтено, что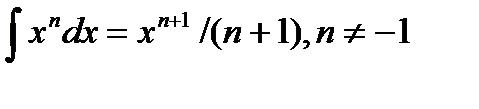

Подставляя (2.16) в исходное уравнение (2.12), получим

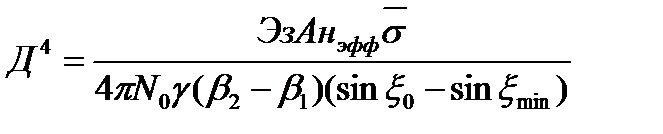(2.17)

2) В процессе обзора изовысотной зоны обнаружения эффективная площадь приемной антенны изменяется в угломестной плоскости по

СТР 17

---------------------------------------------------------------------------------------------------------------------

косеканс – квадратному закону

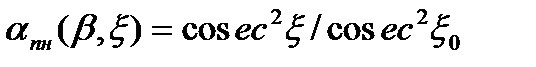при 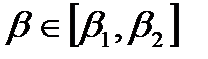(2.18)

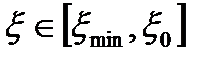
По такому же закону изменяется и коэффициент усиления передающей антенны. Подобное изменение эффективной площади приемной антенны и коэффициента усиления передающей антенны может быть обеспечено, например, за счет выбора конфигурации зеркала антенны в вертикальной плоскости или за счет использования нескольких облучателей, смещенных в угломестной плоскости (приемлемое приближение к косеканс – квадратной ДН можно получить с помощью всего лишь двух облучателей).

Интеграл в уравнении (2.12) для рассматриваемого случая с учетом соотношений (2.15) и (2.18) равен

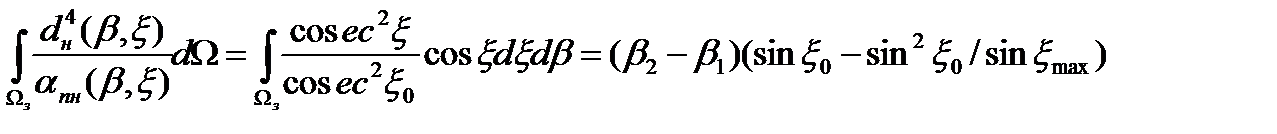(2.20)

и уравнение (2.12) можно представить в виде

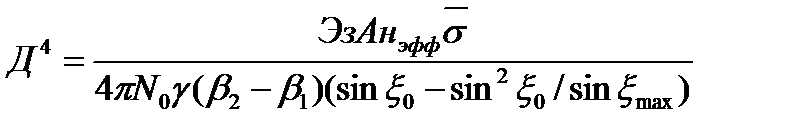
Сравним между собой два рассмотренных варианта формирования изовысотного участка зоны обнаружения по величине энергии, излучаемой в зону за время однократного обзора. При этом будем полагать, что все прочие параметры РЛС в обоих случаях абсолютно одинаковы.

Сопоставим уравнения (2.17) и (2.20)

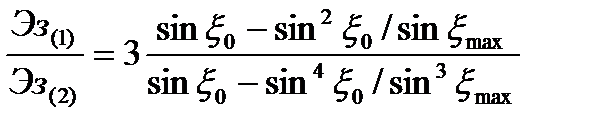
где 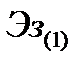и 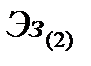- энергии, излучаемые в зону обнаружения при вариантах обзора 2 и 1 соответственно.

При 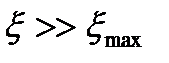(на практике это условие, как правило, выполняется) записанное выше Соотношение можно упростить: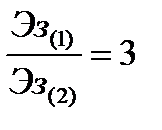

СТР 18

---------------------------------------------------------------------------------------------------------------------

Полученный результат гласит, что с энергетической точки зрения вариант 1 формирования изовысотного участка зоны обнаружения предпочтительнее (выигрыш в энергии зондирующих сигналов составляет около 300%). Кроме тог, следует учитывать и тот факт, что при формировании косеканс-квадратной ДН поверхность антенны во 2 варианте используется неэффективно.

По аналогии со случаем изодальностной зоны интеграл в знаменателе выражения (2.12) можно трактовать как телесный угол некоторой эквивалентной изодальностной зоны обнаружения

Поэтому ,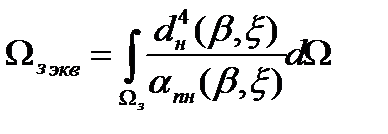

и уравнение радиолокации в режиме обзора зоны обнаружения можно приставлять в виде

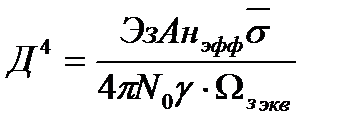(2.21)

Для всей смешанной зоны обнаружения (см. рис. 2.1) интеграл в знаменателе уравнения (2.12) можно представить в виде

,

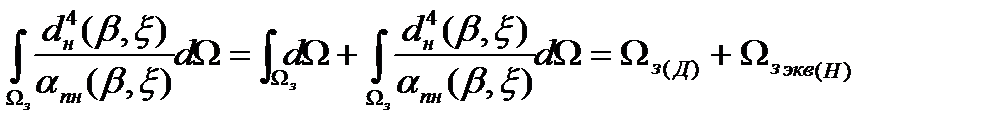где 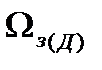- телесный угол изодальностного участка зоны обнаружения;

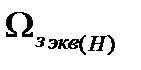- эквивалентный телесный угол изовысотного участка зоны, определяемый по формулам (2.16) или (2.19).

Уравнение радиолокации для смешанной зоны обнаружения принимает вид

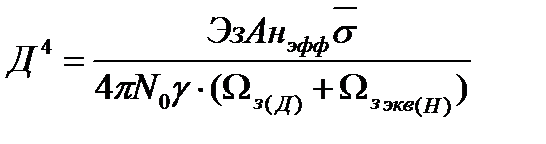(2.22)

СТР 19

---------------------------------------------------------------------------------------------------------------------