Тема: Векторний добуток векторів

Практичне заняття №2

Контрольні питання:

1. Означення векторного добутку.

2. Як обчислюється векторний добуток через координати векторів?

3. Сформулюйте властивості векторного добутку.

4. Де використовується векторний добуток?

Приклади розв’язання задач.

Задача 1. Перетворити вираз .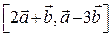

Розв’язання:

Для розв’язання скористаємося властивостями векторного добутку:

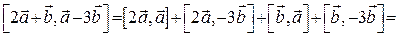
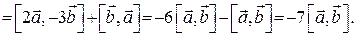
Відповідь: .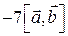

Задача 2. Обчислити координати і модуль вектора 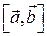, якщо , .

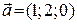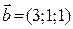Розв’язання:

Векторний добуток обчислюється за формулою:

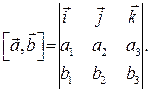
В даному випадку маємо

.

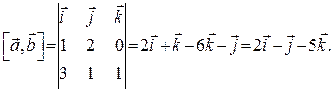
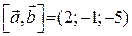Обчислимо тепер модуль вектора :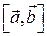

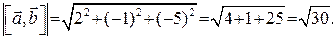
Відповідь: ,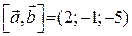

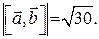
Задача 3. Обчислити площу трикутника 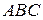, якщо , , .

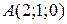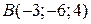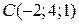Розв’язання:

Площу трикутника визначимо за формулою:

.

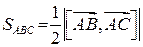Визначимо координати векторів 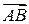і :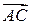

, .

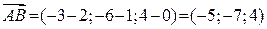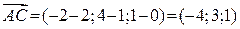Тоді знайдемо векторний добуток векторів 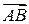і :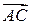

;

.

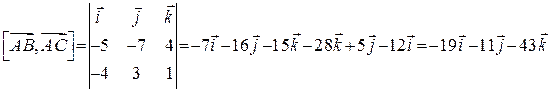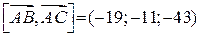Тепер знаходимо модуль вектора :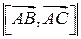

.

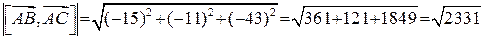Підставивши у формулу для визначення площі, отримаємо:

.

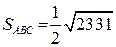Відповідь: 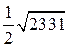(кв.од.).

Задача 4. Обчислити висоту трикутника 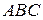, яка проведена з вершини 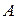, якщо , , .

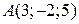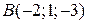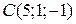Розв’язання:

Скористаємось формулою 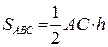, звідки 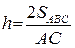. Обчислимо довжину :

.

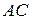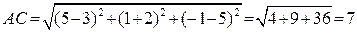Визначимо тепер площу трикутника .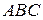

, ;

;

;

;

.

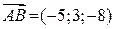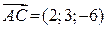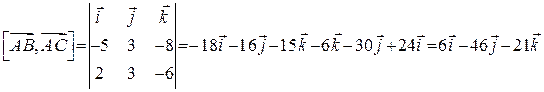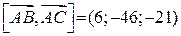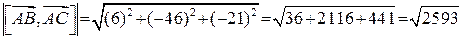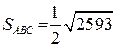Тепер можемо знайти висоту:

.

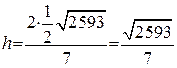Відповідь: 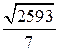(од.).

Задача 5. Обчислити площу паралелограма 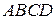, якщо , , , , .

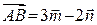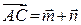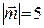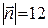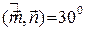Розв’язання:

Площу паралелограма будемо обчислювати за формулою:

.

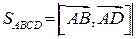Визначимо вектор ; ; .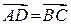

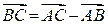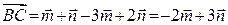Тепер знайдемо векторний добуток:

.

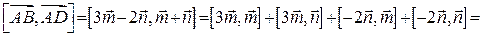
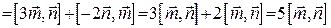Обчислимо модуль вектора :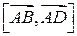

;

.

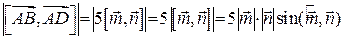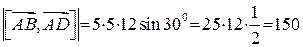Звідси знаходимо, що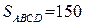

Відповідь: 150 (кв. од.).