Случайной величины

Риск невозможно определить точно, поэтому при оценке риска важное значение имеют статистические методы, позволяющие определить наиболее вероятные величины риска. В статистике такие величины называются характеристиками положения центра распределения случайной величины. Наибольшую практическую значимость имеют три характеристики: математическое ожидание, медиана и мода.

Математическим ожиданием М(ξ) дискретной случайной величины ξ называется взвешенная сумма всех ее возможных значений с весовыми коэффициентами, равными вероятностям этих значений:

_.

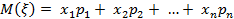Для непрерывной случайной величины имеющей плотность распределения f(х), математическое ожидание определяется формулой:

_.

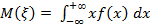Математическое ожидание является мерой центральной тенденции случайной величины, или средним по вероятности ее значением. В физическом смысле, точка с абсциссой х = М(ξ) является координатой центра тяжести фигуры, образованной осью абсцисс и графиком плотности распределения.

Математическое ожидание имеет несколько важных свойств, выполняющихся как для дискретных, так и для непрерывных случайных величин:

1. Математическое ожидание постоянной величины равно этой постоянной:

М(С) = С,

где С — константа.

2. Добавление константы к случайной величине и ее умножение на константу приводят к аналогичным изменениям математического ожидания, т. е. для любых констант а, b и любой случайной величины ξ

.

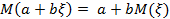3. Для любых случайных величин ξ и η математическое ожидание их суммы равно сумме их математических ожиданий:

.

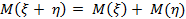4. Если случайные величины ξ и η независимы, то математическое ожидание их произведения равно произведению их математических ожиданий:

.

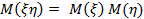В некоторых случаях наиболее информативной характеристикой случайной величины является не средневероятное, а наиболее часто встречающееся ее значение. Такая характеристика называется модой. Распределение может иметь не один, а несколько локальных максимумов вероятности, — такое распределение называется мультимодальным, или полимодальным (рис. 4.16). Распределение с единственным максимумом плотности вероятности называется унимодальным. Для симметричных унимодальных распределений значения математического ожидания и моды совпадают.

Еще одна практически важная обобщенная характеристика распределения — медиана. Медианой случайной величины ξ называется такое значение q, для которого ξ с равной вероятностью принимает значения, меньшие q и большие q, т. е.

= = .

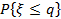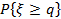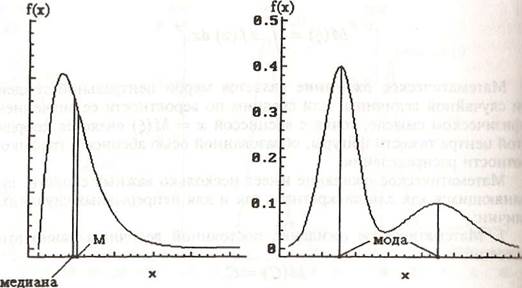
Рис. 4.15. Математическое ожидание Рис. 4.16. Мода распределения случайной

(М) и медиана – случай несимметричного величины – случай бимодального распре-

Распределения деления

В случае непрерывной случайной величины прямая х = q делит фигуру, ограниченную функцией плотности, на две части с равными площадями.

Медиана, как и математическое ожидание, может рассматриваться в качестве характеристики общей тенденции случайной величины Для симметричных распределений медиана совпадает с математическим ожиданием, а если к тому же распределение унимодально, то и с модой. В частности, для нормального распределения математическое ожидание, медиана и мода равны параметру распределения а. Несовпадение медианы с математическим ожиданием служит простейшим признаком асимметричности распределения случайной величины (рис. 4.15).