1. Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций:
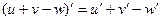 .
.
2. Производная произведения двух дифференцируемых функций равна сумме произведения производной первого множителя на второй множитель и произведения первого множителя на производную второго:
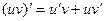 .
.
Следствие 1. Постоянный множитель можно вынести за знак производной: 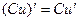 .
.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
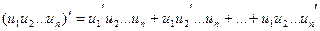 .
.
3. Производная частногодвух дифференцируемых функций может быть найдена по формуле: 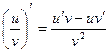 (
(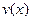
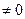 ).
).
Докажем, например, правило 2 (правила1-3 докажите самостоятельно).
Рассмотрим функцию 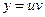 . Дадим аргументу
. Дадим аргументу 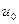 приращение
приращение 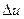 , аргументу
, аргументу 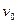 приращение
приращение 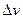 . Соответственно, их произведение получит приращение
. Соответственно, их произведение получит приращение
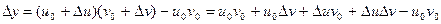 .
.
Составим отношение 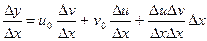 . Переходя в этом равенстве к пределу при
. Переходя в этом равенстве к пределу при 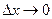 , получим:
, получим:
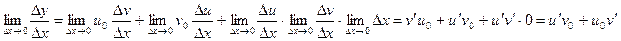
4. Дифференцирование обратной функции.
Если функция 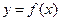 имеет обратную функцию
имеет обратную функцию 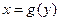 и
и 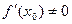 , то обратная функция дифференцируема в точке
, то обратная функция дифференцируема в точке 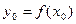 , причем
, причем
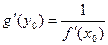 .
.
5.
Дифференцирование сложной функции.
Если функции 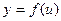 и
и 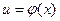 дифференцируемы по своим аргументам, то производная сложной функции
дифференцируемы по своим аргументам, то производная сложной функции 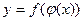 существует и равна произведению производной внешней функции по промежуточному аргументу и производной промежуточного аргумента по независимой переменной:
существует и равна произведению производной внешней функции по промежуточному аргументу и производной промежуточного аргумента по независимой переменной: 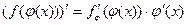 .
.
Таким образом, производные сложных функций можно вычислить по формулам:
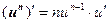
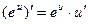
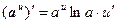
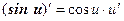
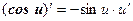
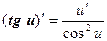
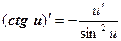
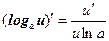
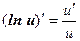
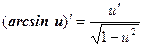
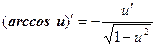
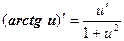
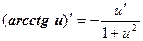
Пример. Найти производную функции 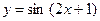 .
.
 2015-07-14
2015-07-14 463
463








