Пусть функция 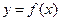 определена на промежутке Х и дифференцируема в некоторой окрестности точки
определена на промежутке Х и дифференцируема в некоторой окрестности точки 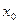
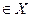 .
.
Тогда существует конечная производная 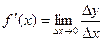 .
.
По теореме о связи предела и бесконечно малой:
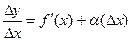 , где
, где 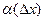 - бесконечно малая при
- бесконечно малая при 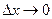 . Отсюда
. Отсюда
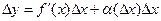 .
.
Таким образом, приращение функции можно представить в виде суммы двух слагаемых: линейного относительно 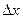 и бесконечно малого при
и бесконечно малого при 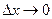 .
.
Опр. Дифференциалом функции называется главная, линейная относительно 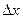 часть приращения функции, равная произведению производной на приращение аргумента:
часть приращения функции, равная произведению производной на приращение аргумента:
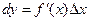 .
.
Рассмотрим функцию у=х и найдем ее дифференциал.
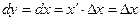 . Таким образом, формула дифференциала может быть записана в виде:
. Таким образом, формула дифференциала может быть записана в виде:
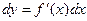 .
.
Пример. Найти дифференциал функции 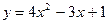 .
.
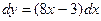 .
.
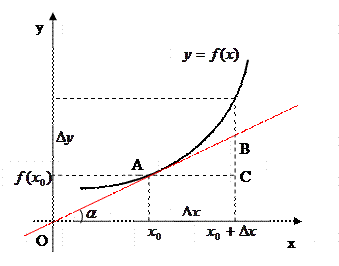
Выясним геометрический смысл дифференциала. Из 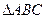 :
: 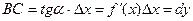 . Таким образом, дифференциал есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение
. Таким образом, дифференциал есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение 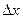 .
.
 Свойства дифференциала аналогичны свойствам производной:
Свойства дифференциала аналогичны свойствам производной:
1. d(С)=0;
2. d(u+v)=du+dv;
3. d(uv)=vdu+udv;
4. 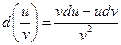 ;
;
5. Форма дифференциала инвариантна (неизменна): он всегда равен произведению производной на дифференциал аргумента, независимо от того, простым или сложным является аргумент.
Пример 1. Найти дифференциал функции 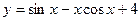 .
.
Решение. Используя свойства дифференциала, получим: 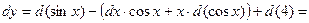
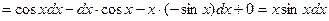 .
.
Пример 2. Найти дифференциал функции 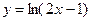 .
.
Решение. 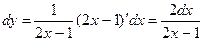 .
.
Опр. Дифференциалом второго порядка (или вторым дифференциалом) 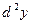 называется дифференциал от дифференциала функции, т.е.:
называется дифференциал от дифференциала функции, т.е.:
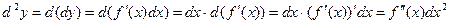 .
.
Аналогично, дифференциалом п -го порядка называется дифференциал от дифференциала (п-1) -го порядка этой функции: 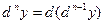 .
.
 2015-07-14
2015-07-14 379
379







