Постановка задачи

НА ОСНОВЕ АППРОКСИМАЦИИ ДАННЫХ

Эмпирические модели формируются по результатам эксперимента (на основании данных наблюдений). Моделируемый объект рассматривается как «черный ящик». Для измерения доступны только его входные и выходные сигналы. Ставится задача - на основе обработки результатов измерений входных и выходных сигналов объекта выявить эмпирические закономерности в полученных данных и математически описать их формальной приближенной аналитической моделью.

В инженерной практике и в научных исследованиях часто приходится решать следующую задачу.

В результате серии измерений величин x и y получены m пар значений x_i; y_i (i = 1, 2, 3, …, m), которые представлены в табличной форме. Полагают, что x – независимая переменная, а y – зависимая переменная. Требуется установить функциональную зависимость между x и y, т.е. определить такую приближенную аналитическую формальную модель, которая бы наиболее соответствовала данному набору экспериментальных данных x_i; y_i (i = 1, 2, 3, …, m).

Задача аналитического приближения таблично заданных функций представляет одну из категорий задач аппроксимации.

Под аппроксимацией понимают приближение (приближенную замену) исходной функции другой функцией, более простой и легко вычисляемой.

Решение задачи аналитического приближения таблично заданной функции предполагает следующие действия.

1. Выбор класса аппроксимирующей функции – эмпирической модели, , наилучшим образом отражающей связь между экспериментальными данными x и y.

2. Оценивание (нахождение числовых оценок) параметров a₀, a₁, a₂, …, a_n приближающей функции с учетом того, что результаты измерений x_i; y_i получены с некоторой погрешностью.

Приближающую функциональную зависимость называют эмпирической формулой или уравнением регрессии. График приближающей функции называют линией регрессии.

Определение аналитического выражения для описания связи зависимой величины y с независимыми величинами (факторами) x ₁, x ₂, …,x_m – называют задачей регрессионного анализа.

Для определения параметров эмпирической модели воспользуемся методом наименьших квадратов.

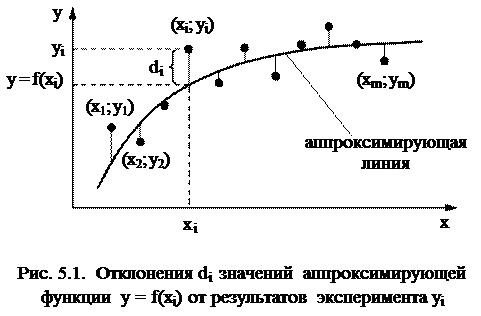Метод наименьших квадратов обеспечивает нахождение параметров эмпирической модели 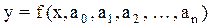на основе критерия минимума суммы квадратов отклонений d_i (i = 1, 2, 3, …, m) значений приближающей функции (значений, предсказанных моделью) от результатов эксперимента y_i(см. рис. 5.1).

С точки зрения метода наименьших квадратов наилучшее согласование линии регрессии с результатами измерений y_i достигается при выполнении условия

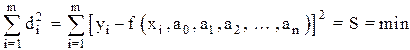. (5.1)

Необходимым условием минимума функции S = S(a₀, a₁, a₂, …, a_n) является равенство нулю ее частных производных по всем переменным. Поэтому задача нахождения параметров a₀, a₁, a₂, …, a_n эмпирической модели сводится к решению следующей системы уравнений

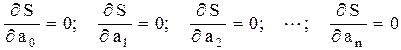. (5.2)

При решении задачи линейной регрессии, когда результаты эксперимента приближаются линейной функцией вида y = a x + b, система уравнений (5.2) принимает вид

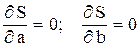. (5.3)

После соответствующих подстановок система (5.3) приводится к следующему виду

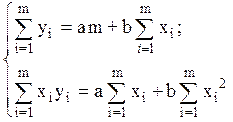(5.4)

Решая систему (5.4) находят искомые значения параметров a и b регрессионной модели:

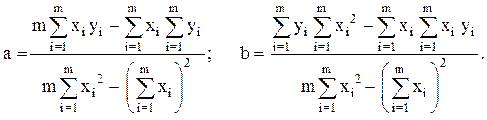(5.5)

Оценить степень отклонения связи между x_i и y_i от линейной (или тесноту линейной связи) можно с помощью коэффициента парной корреляции (коэффициента корреляции Пирсона)

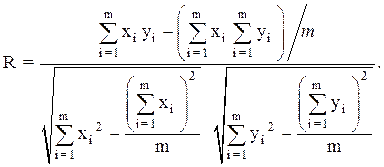(5.6)

Чем ближе значение коэффициента R по абсолютной величине к единице, тем сильнее проявляется линейная зависимость между x_i и y_i, и, следовательно, тем лучше экспериментальные точки согласуются с линейной моделью. Считается, что при 0,9 < |R| < 0,99 – очень сильная теснота линейной связи; при 0,7 < |R| < 0,9 – сильная; при 0,5 < |R| < 0,7 – заметная; при 0,3 < |R| < 0,5 – слабая теснота линейной связи.

Поиск эмпирической функции в виде полинома (многочлена)

,

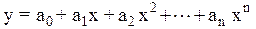называют решением задачи полиномиальной регрессии. Достоинство полиномов в том, что они являются линейными функциями относительно своих коэффициентов.

Рассмотрим частный случай, когда результаты эксперимента приближаются (аппроксимируются) полиномом второй степени

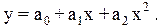(5.7)

Значения (оценки) коэффициентов a₀, a₁, a₂ согласно методу наименьших квадратов определяем из условия

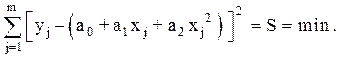(5.8)

Минимизируем функцию S, приравнивая нулю ее частные производные по каждому из коэффициентов:

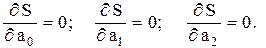(5.9)

В итоге приходим к системе уравнений (СЛАУ)

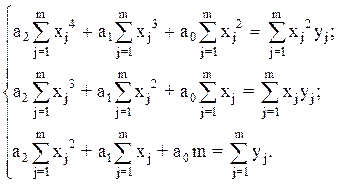, (5.10)

решая которую находим искомые значения (оценки) параметров a₀, а₁, а₂ регрессионной модели (5.7).