На рис.55 приведены параметры движения авиабомбы ФАБ-500 М-62, сброшенной с высоты 20000 м на скорости, соответствующей числу
М = 1,5.
X,Y, км М






 50
50
 |

 40
40
 X
X
 30
30

 M Y
M Y


 20 2
20 2
 |
 10 1
10 1
 20 40 60 80 t
20 40 60 80 t
Рис.55
Во всем диапазоне чисел М полета АБ должна быть устойчива, т.е. обладать способностью после действия возмущения возвращаться в положение, при котором ее ось совпадает с касательной к траектории и возникающие при этом колебания должны носить затухающий характер.
Рассмотрим силы и моменты, действующие на АБ в свободном полете (рис.56).



 У R
У R
 |



 Уа Xа
Уа Xа



 Х
Х










 цт цд
цт цд

 a
a
 V Хцд
V Хцд

Рис.56
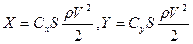
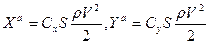
Cсоотношения между коэффициентами в связанной и поточной системами координат следующие
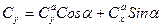
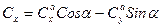
Восстанавливающий момент 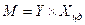 у статически устойчивых грузов направлен в сторону уменьшения угла атаки.
у статически устойчивых грузов направлен в сторону уменьшения угла атаки.
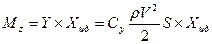 или
или 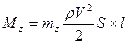
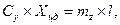
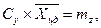
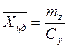
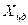 в % называется запасом статической устойчивости, для авиабомб обычно запас составляет 5…10%.
в % называется запасом статической устойчивости, для авиабомб обычно запас составляет 5…10%.
Характер изменения зависимости 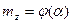 характеризует устойчивость авиабомб (рис.57).
характеризует устойчивость авиабомб (рис.57).
mz
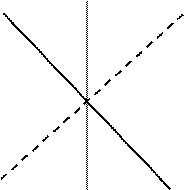
устойчивая АБ
 |
 a
a
не устойчивая АБ
|
|
|
 |
Рис.57
Авиабомба должна обладать динамической устойчивостью. Под динамической устойчивостью понимается способность АБ к затухающим колебаниям.
Представим авиабомбу в виде пластины, центр давления которой расположен на расстоянии 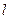 (рис.58).
(рис.58).
 Y
Y
 |
w a
 |
Рис.58
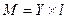 ;
; 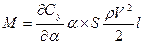
Определим суммарную скорость и приращение угла атаки пластины в колебательном движении (рис.59).
 |



 V 90 + a
V 90 + a
Da w´l

 V VS
V VS
 |
 a
a
Рис.59
Из теоремы косинусов 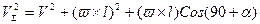 . Предположим, что
. Предположим, что 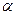 мало и
мало и 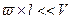 , отсюда
, отсюда 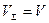
Из теоремы синусов определим 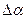 .
.
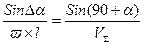
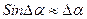 , отсюда
, отсюда 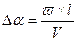 , таким образом
, таким образом 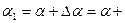
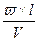
Подставим выражение суммарного угла атаки в выражение для момента


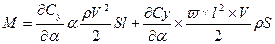
 | |||
 | |||
восстанавливающий демпфирующий
момент момент
или 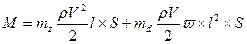

Cоставим уравнение углового движения
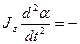
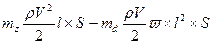
Обозначим 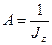 ,
, 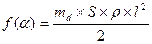 ,
, 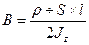
отсюда 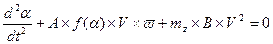 .
.
Обозначим 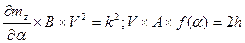
отсюда 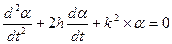
Коэффициенты 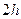 и
и 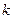 при
при 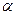 = ± 300 постоянны, поэтому уравнение колебаний является уравнением второго порядка с постоянными членами (уравнение свободных колебаний) и его решение
= ± 300 постоянны, поэтому уравнение колебаний является уравнением второго порядка с постоянными членами (уравнение свободных колебаний) и его решение
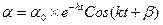
где 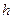 – декремент затухания,
– декремент затухания, 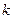 - круговая частота
- круговая частота 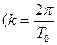 ),
), 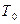 – период
– период
колебаний, 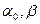 - постоянные.
- постоянные.
При 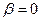 и
и 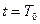
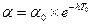
Отсюда декремент затухания 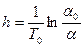
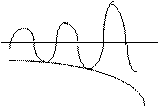
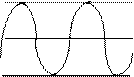
Декремент затухания характеризует колебательный процесс (рис.60).
 | |||
 |
 | |||||
 | |||||
 | |||||
h > 0 h = 0 h < 0
Рис.60
По периоду или длине волны можно судить о степени статической устойчивости.
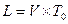
Из теории колебаний известно, что частота затухающих колебаний равна
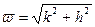
При движении АБ в воздухе 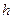 мало, отсюда
мало, отсюда 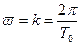
но 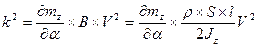 ,
, 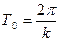
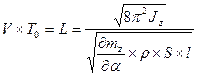 ,
, 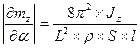
Из практики известно, если L = 30…100 м, то АБ устойчива.
 2015-07-14
2015-07-14 914
914








