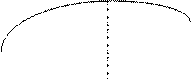
Начальная скорость осколка определяется экспериментальным путем и расчетами. Так как взрывная нагрузка распределяется вдоль оболочки неравномерно, то начальная скорость осколков, образованных из различных сечений, будет различной (рис.48).
 Vo
Vo
 |
Vmax

 х
х
 | |||
 |
Рис.48
Рассмотрим цилиндрическую оболочку бесконечной длины и вырежем из нее элемент длиной Dh (рис.49).
r 




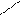






 m0
m0

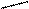


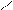
 ∆h
∆h
 V
V



 Vo
Vo
 r
r
Рис.49
Скорость радиального расширения продуктов детонации (в момент разрушения оболочки, непосредственно примыкающих к ней) будет 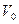 . Скорость радиального движения продуктов детонации во внутренних слоях будет меньше
. Скорость радиального движения продуктов детонации во внутренних слоях будет меньше 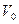 (от 0 до
(от 0 до 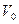 ). Можно предположить, что
). Можно предположить, что 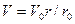 .
.
Определим кинетическую энергию продуктов детонации 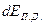 , заключенных в элементарном объеме толщиной
, заключенных в элементарном объеме толщиной  , радиус которого равен
, радиус которого равен 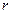 .
.
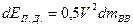
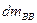 – масса продуктов детонации элементарного слоя (масса ВВ).
– масса продуктов детонации элементарного слоя (масса ВВ).
Очевидно 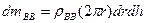 , отсюда
, отсюда
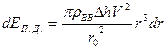
Интегрируя, получим
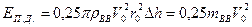
Продуктами детонации вовлечена в движение оболочка. Ее кинетическую энергию можно записать
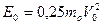
Движение продуктов детонации и осколков происходит за счет потенциальной энергии ВВ
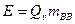
Если положить, что вся энергия тратится на сообщение скорости продуктам детонации и на метание осколков, то на основе закона сохранения энергии, запишем
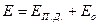
Отсюда
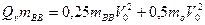
Решая относительно 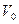 , получим
, получим
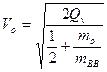
Выразим 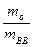 через коэффициент наполнения
через коэффициент наполнения 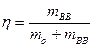
отсюда
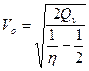
Формула получена без учета потерь энергии на разрушение оболочки и сообщения продуктам детонации скорости в осевом направлении. Расчеты показывают. Что потерями энергии на разрушение оболочки можно пренебречь. Потери энергии за счет истечения с торцов заряда зависят от относительных размеров заряда. Чем короче заряд – тем больше потери. Величина этих потерь зависит и от абсолютных размеров заряда.
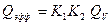
где 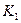 – коэффициент, учитывающий потери в зависимости от относительного размера заряда;
– коэффициент, учитывающий потери в зависимости от относительного размера заряда;
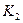 – коэффициент, учитывающий потери энергии в зависимости от массы заряда.
– коэффициент, учитывающий потери энергии в зависимости от массы заряда.
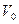 зависит от
зависит от 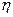 и
и 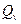 , закрытие торцев заряда увеличивает
, закрытие торцев заряда увеличивает 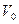 , повышение прочности оболочки – уменьшает.
, повышение прочности оболочки – уменьшает.
 2015-07-14
2015-07-14 675
675








