Аналогично доказательству утверждения 3

Из утверждений 1,2, 3 и 4 следует первая часть теоремы, т.е., что в HS4 имеется всего 6 несводимых модальностей.

3). Докажем справедливость в HS4 шести импликаций, образующих схему из формулировки теоремы.

а) □ A □ ◊ □ A

б) □ ◊ □ A ◊ □ A

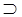в) □ ◊ □ A □ ◊ A

г) ◊ □ A 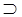◊ □ ◊A

д) □◊ A 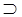◊ □ ◊A

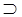е) ◊ □ ◊A ◊A

Все они доказываются аналогично утверждениям 3 и 4.

Например, докажем импликацию а):

1. □ А ≡ □□□ А по утверждению 1,

2. Достаточно доказать □□□ А □◊□ А

3. По ВП3 достаточно доказать □□ А ◊□ А

но □ В ◊ В, для любой формулы В, т.к.

□В В и В ◊В – аксиомы А3.