Следствие

Структура неприводимых модальностей в S4.

Теорема. В системе S4 существует шесть несводимых модальностей □ A, □ ◊ □ A,

◊ □ A, □ ◊ A, ◊ □ ◊A, ◊A причем их логическая сила определяется следующей диаграммой:

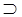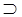
◊ □ A

□ A 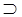□ ◊ □ A ◊ □ ◊A ◊A.

□ ◊ A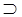

Доказательство.

1). Сначала покажем, что в HS4 справедливы следующие вспомогательные правила.

ВП1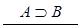

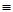□ А □ В □ А □ В

ВП2

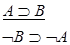
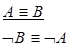
ВП3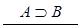

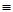◊А ◊ В ◊А ◊ В

ВП1

1. 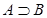доказано.

2. □ (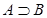) по правилу введения □

3. □ (А В) (□ А □ В) аксиома А2

4. □А □В правило MР. 2,3.

Для 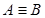аналогично.

ВП2

1. 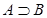доказано,

2. 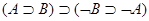аксиома А0,

3. правило МР 1,2,

Для 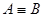аналогично.

ВП3

1. 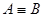доказано,

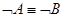2. ВП2,

3. □ 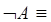□ 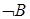ВП1,

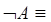
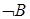4. □ □ ВП2.

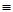◊ есть сокращение для □ . Следовательно, ◊А ◊ В.

2). Докажем справедливость следующих утверждений в HS4.

Утверждение 1. □ □ А ≡ □ А

Доказательство:

1. □□А □Ааксиома А1,

2. □А □□А аксиома А3,

3. (□□А □А) ((□А □□А) (□□ А ≡ □ А)) аксиома А0,

4.□□ А ≡ □А 2 раза правило МР.

Следствие.

□…□ А ≡ □А

^{к раз}

Утверждение2. ◊◊А≡◊А

Доказательство:

◊ есть сокращение для □ .

Тогда справедлива следующая цепочка эквивалентностей:

◊◊А ≡ □ □ А ≡ □ □ А ≡ □ А ≡ ◊А