2015-07-14
271
Московский государственный технический университет
Им. Н.Э. Баумана
Калужский филиал
Кафедра К5 - КФ
МЕТОД СЕЧЕНИЙ ПРИ РАСТЯЖЕНИИ, СЖАТИИ И КРУЧЕНИИ
(Методические указания по технической механике
Составитель: Борискин О.Ф.
Калуга 2002
1. Расчет статически определимых стержней на растяжение и сжатие
1.Задача:
Для стального ступенчатого стержня (А и 2А площади ступеней) длиной 4l, на- груженного системой сил N, нормальных напряжений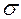 
и осевых перемещений W.
Решение:
Определим опорную реакцию.
Введем прямоугольную систему координат с центром О в жесткой заделке и направим ось Z вправо. Запишем уравнение равновесия для всего стержня:
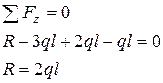
Распределение нормальных сил.
Используя метод сечений, рассмотрим последовательно все четыре участка стержня.
1.2.1. Рассечем брус на участке ВС, отбросим его правую часть и рассмотрим равновесие левой части бруса, нагруженной на конце силой 2ql и внутренней силой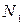 
(рис. 2б). Направим силу внутреннего взаимодействия (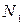) вдоль оси Z. Запишем уравнение равновесия для данной части бруса:
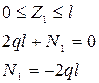
На эпюре нормальных сил (рис. 2е) отложим от нулевой линии вниз координаты, равные в некотором масштабе ql.
1.2.2. Проведем сечение на участке CD (рис. 2в), отбросим правую часть бруса и приложим к отсеченной части внешние и внутренние силы. Запишем условие равновесия:
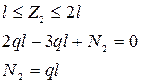
1.2.3. На участке DE проведем сечение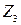 
и отбросим правую часть. Этот участок нагружен равномерно распределенными внешними силами, поэтому внутренняя сила в сечениях этого участка зависит от положения сечения (рис. 2г)
. 
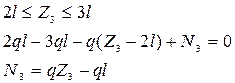
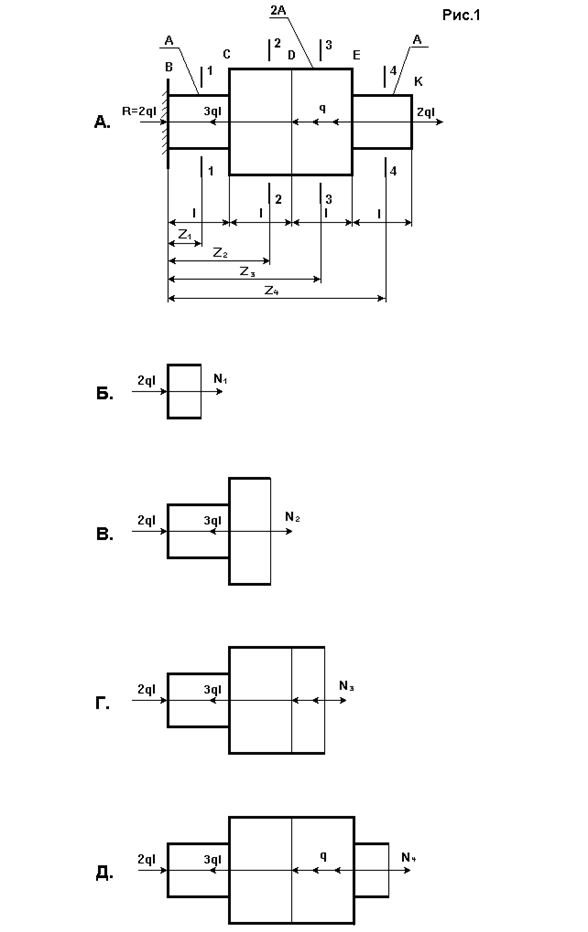
Рис. 2
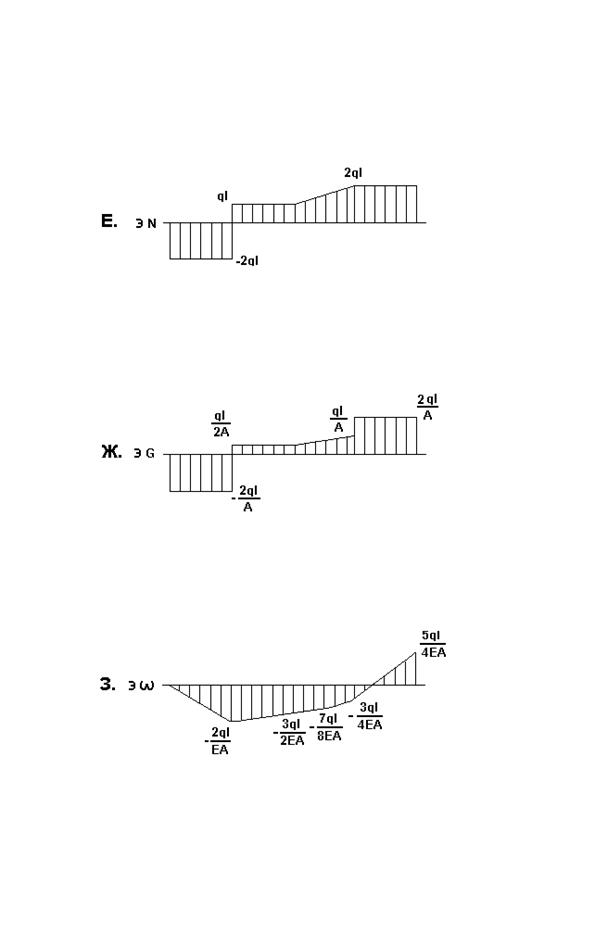
Рис. 2 (продолжение)
Найдем значения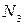 
на границах интервала:
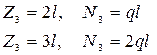
Аналогично на участке ЕК построим сечение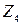 
(рис. 2д):
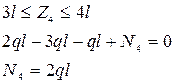
Окончательная эпюра нормальных сил приведена на рис. 2е.
