Теорема Остроградского –Гаусса в диэлектрической среде формулируется в следующем виде
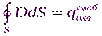
Для произвольной замкнутой поверхности S поток вектора смещения электростатического поля D сквозь эту поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов (вектором D описывается электростатическое поле, создаваемое свободными зарядами, но при таком их распределении, какое имеется при наличии диэлектрика).
Условия для ЭСП на границе раздела диэлектриков
На границе раздела двух изотропных диэлектрических сред с диэлектрическими проницаемостями ε1 и ε2. Векторы напряженности поля Е и электрического смещения D связаны соотношениями
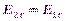 и
и 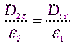
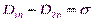 и
и 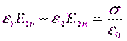
где Еτ и Dτ – проекции векторов Е и D на единичный вектор τ, касательный к границе раздела сред, Еn и Dn – проекции векторов Е и D на единичный вектор n, проведенный по нормали к поверхности раздела сред, σ – поверхностная плотность свободных зарядов.
Если поверхность специально не наэлектризована, то
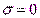 →
→ 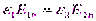 и
и 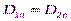
и, если одна среда – вакуум, то
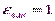 →
→ 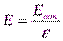
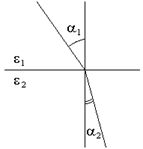
При переходе через границу раздела силовые линии преломляются. Если 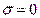 , то
, то
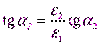
Если поверхность раздела совпадает с эквипотенциальной поверхностью, то
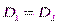 и
и 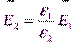
 2015-07-14
2015-07-14 608
608







