Вопросы и задания для самостоятельной работы 8 страница

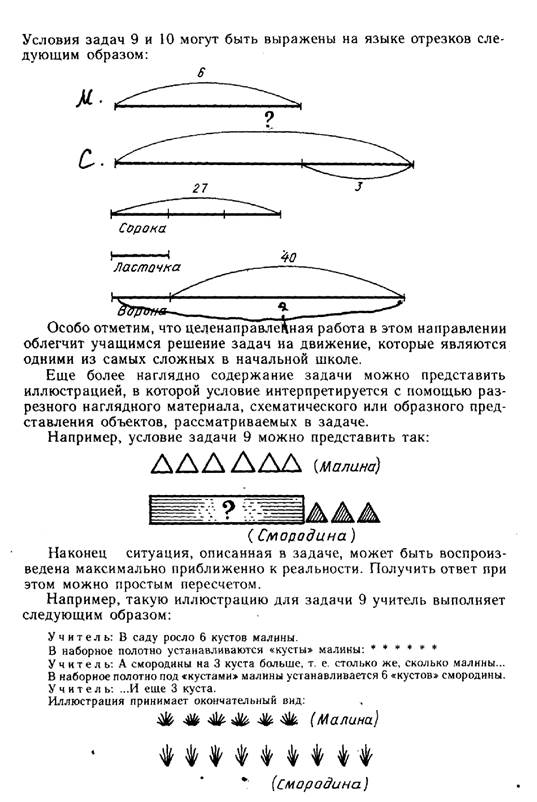
Предметное воссоздание условия задачи, допускающее получение ответа с помощью пересчета, может использоваться, за редким исключением, только в первом классе. Причем либо при знакомстве учащихся с новым сложным понятием, либо при работе со слабоуспевающими учащимися. В связи с рассмотренными видами интерпретации условия задачи сделаем некоторые замечания.

1. Как известно из психологии, обучение в наибольшей степени выполняет развивающую функцию, если учебный материал преподается учащимся на высоком уровне трудности. Поэтому переход к новому, более наглядному виду интерпретации условия текстовой задачи должен осуществляться только тогда, когда ученики испытывают непреодолимые трудности в поисках решения данной задачи.,, Следовательно, первоначально условие задачи может быть представлено в виде краткой записи, и только потом, по мере необходимости, можно переходить к другим видам наглядности — чертежу, геометрической интерпретации, реальной модели.

2. Реальная модель может быть создана, конечно, не для любой задачи. Как правило, этому препятствуют большие числовые значения или невоспроизводимые в условиях урока явления, рассматриваемые в задаче. В таком случае решается аналогичная задача, лишенная названных недостатков. После того как найдена идея решения, ее применяют к исходной задаче.

Поясним смысл этих замечаний на конкретном примере.

Пусть на уроке учащимся предложена следующая задача: «На одном тракторе работали в течение 60 ч, а на другом — 55 ч. При одинаковом расходе горючего на первом тракторе было израсходовано на 35 л горючего больше, чем на втором. Сколько горючего было израсходовано на каждом тракторе?»

Предположим, что после анализа текста данной задачи учащиеся не в состоянии найти ее решение. В таком случае под руководством учителя они приступают к краткой записи условия. В процессе анализа условия выделяются величины: время работы тракторов, расход горючего в единицу времени (в час), общий расход горючего. Определяется также, какие числовые значения соответствуют этим величинам. Краткое условие может быть записано в следующем виде:

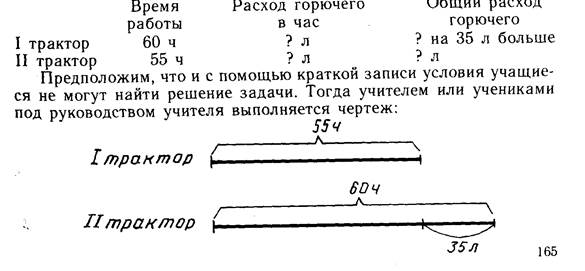
Из чертежа видно, что разности расхода горючего соответствует разность времени работы тракторов. Поэтому уже нетрудно заметить, как определить расход горючего в час.

Если и чертеж не помогает учащимся найти решение задачи, можно перейти к еще более наглядной интерпретации условия с помощью наборного полотна и разрезных фигур. Однако если, например, норму расхода горючего в час обозначить каким-либо символом, то иллюстрация получится чрезвычайно громоздкой. Поэтому вместо исходной задачи рассматривается и иллюстрируется аналогичная ей, но с другими числовыми данными: «На одном тракторе работали в течение 5 ч, на другом З ч. При одинаковом расходе горючего на первом тракторе было израсходовано на 4 л горючего больше, чем на втором. Сколько горючего было израсходовано на каждом тракторе?»:

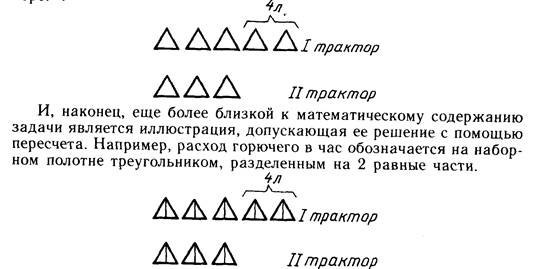
Иногда при работе над задачей необходимо использовать одновременно два вида интерпретаций. Пусть, например, дана задача:

«Из пунктов А и Б одновременно навстречу друг другу выехали два автомобиля. Один двигался со скоростью 50 км в час а другой

70 км в час. Через 5 ч автомобили встретились. Определить расстояние между А и Б».

для того чтобы учащиеся смогли самостоятельно найти решение 50. 5+70 5, достаточным, возможно, окажется выполнение чертежа. Но для того чтобы ученики увидели более рациональное решение этой задачи (50+70). 5, нужно объяснить им, что такое скорость сближения и как она выражается математически. Это потребует от учителя использования подвижной модели, т. е. реального воспроизведения характера движения автомобилей.

Навыки выполнения краткой записи условия задач, чертежей по условию задач, приобретенные учащимися в начальной школе, будут полезны им и при решении математических задач в средних и старших классах.

Поиск решения задачи. Решение задач — сложная интеллектуальная Деятельность. Описать ее содержание в полном объеме невозможно, даже если иметь в виду деятельность, осуществляемую младшим школьником.

По существу поиск решения задачи начинается уже при анализе текста задачи и не заканчивается даже тогда, когда ответ получен и проверен. Идея нового способа решения может прийти тогда, когда, казалось бы, получен исчерпывающий ответ на вопрос задачи.

Здесь мы не будем рассматривать внутренние, психические механизмы умственной деятельности ученика, ищущего решение задачи,— это могло бы стать предметом целой книги. Опишем только внешнюю сторону деятельности ученика, который, уже познакомившись с величинами и отношениями, рассматриваемыми в задаче, приступает к поиску математического выражения ее содержания. Остановимся также на общих методических приемах, которыми пользуется учитель, побуждая учащихся к такой деятельности.

В начальной школе обучение учащихся поиску решения задач осуществляется на двух уровнях. Характер деятельности ученика и учителя на каждом пути различен.

Сначала учащиеся учатся находить решение простых задач в одно действие. Умение найти решение такой задачи заключается в том, что ученик может поставить в соответствие отношению, которое связывает числовые данные задачи, арифметическое действие. Например, в задаче: «Скорость автомобиля 80 км в час, а скорость велосипедиста в 4 раза меньше. Определить скорость велосипедиста» две величины — скорость автомобиля и скорость велосипедиста связаны отношением «в... раз больше». Поиск ее решения сводится к выбору действия умножения в соответствии со смыслом данного отношения.

Таким образом, обучение поиску решения простых задач и заключается в формировании у учащихся умения определять, какое арифметическое действие соответствует тому или иному реальному отношению.

Более высокий уровень обучения поиску решения задач осуществляется на множестве составных задач, решаемых в несколько действий.

На первый взгляд может показаться, что для ученика, который умеет решать простые задачи, решение составной задачи не представляет трудности: ведь нужно по существу последовательно решить несколько простых задач. Однако на самом деле все гораздо сложнее.

Рассмотрим задачу: «Пионеры собрали 80 кг макулатуры, а октябрята — на 20 кг меньше. Сколько макулатуры собрали оба отряда вместе?» В условии простой задачи известны, как правило, два числовых значения каких-либо величин и некоторое отношение, которое их связывает. В данной задаче также известны два числовых значения и два отношения — «на... меньше» и «оба... вместе». Ученик, умеющий решать простые задачи, знает, что если «на... меньше», то нужно выполнить вычитание, а если оба... вместе»,— сложение. Но для решения приведенной задачи этих знаний недостаточно. Нужно еще определить, разность значений каких величин необходимо вычислить; сумму значений каких величин необходимо найти. Таким образом, поиск решения составных задач качественно отличается от поиска решения простых задач. Качественно другой должна быть и методика обучения поиску решения составных задач.
Классифицировать составные задачи по типам соответствующих им числовых выражений нецелесообразно*. Поэтому система составных задач, решаемых в начальной школе, очерчена весьма условно:
это задачи, требующие выполнения не более трех действий, в их числе задачи на пропорциональность и на движение. Это обстоятельство и обусловливает основную особенность методики обучения учащихся поиску решения составных задач. Эта методика должна быть ориентирована на формирование у учащихся общих методов поиска решения, соответствующих интеллектуальным возможностям младших школьников. К таким методам относятся аналитический, синтетический и аналитико-синтетический.
Аналитический метод. Анализ логический прием, состоящий в расчленении исследуемого объекта на составные элементы в исследовании каждого из них в отдельности. Он может использоваться многократно.
В задаче исследуемый объект описывается в требовании. Однократно или многократно расчленяя объект, приходят, наконец, к составляющим, которые даны в условии задачи (если, конечно, данная задача имеет решение).
Аналитический метод состоит в многократном последовательном использовании анализа. Применительно к текстовым задачам аналитический метод позволяет расчленить составную задачу на систему простых задач. Поясним это на примере.
За да ч а 12. За 4 м сукна заплатили столько же, сколько за 14 м шелка. Цена шелка б р. за метр. Какова цена сукна?
Расчленим объект, описываемый в требовании. Для этого воспользуемся следующим соображением: чтобы определить цену сукна, достаточно взять количество купленного сукна и его стоимость. Другими словами, достаточно решить простую задачу, в условии которой сказано, сколько купили сукна и сколько за него заплатили. В исходной задаче первая величина известна, а вторая — нет. Поэтому повторно используем прием анализа: выясним, какие компоненты определяют стоимость сукна.
* Пусть, например, составные задачи классифицированы по следующему принципу: задачи относятся к одному типу, если их содержание описывается числовыми выражениями, имеющими одинаковый вид (а + Ь + с, или а + Ь — с, или а:Ь + с — й и т. д.). Так, задачи: В колхозной бригаде 5 гусеничных тракторов, а колесных на З больше. Сколько всего тракторов в бригаде и <В школе работают З спортивные секции: легкоатлетическая, гимнастическая и футбольная. В легкоатлетической занимается 15 школьников, в гимнастической — 27, а в футбольной — на 9 человек больше, чем в легкоатлетической и гимнастической вместе. Сколько человек занимается в футбольной секции? относятся к одному типу, так как их общий вид: а + Ь + с.
Определим, какое количество типов задач, решаемых в два действия, возможно щи такой классификации. Воспользуемся формулой для размещений с повторениями А4= 42, де 4— количество арифметических операций; 2 — количество операций, необходимых для решения каждой задачи. Задачи в три действия подразделяются на 64 типа (А = 4). Таким образом, классификация составных задач содержала бы 80 (!) типов задач и, конечно, были бы неприменима на практике. -

В исходной задаче сказано, что за сукно заплатили столько же, Сколько за шелк. Значит, нужно решить простую задачу, в условии которой даны количество купленного шелка и его цена. Значения и той и другой величины известны из условия исходной задачи.
Итак, составная задача с помощью аналитического метода расчленена на две простые задачи, причем ответ к одной из них является данным условия другой: «Купили 14 м шелка по цене б р. за метр. Сколько стоит купленный шелк? и «Купили 4 м сукна и заплатили? рублей (столько же, сколько за шелк). Какова цена сукна?
Поиск решения задачи, осуществляемый младшим школьником, можно рассматривать как следующий процесс: ученик задает себе вопросы и отвечает на них. В таком случае обучение поиску решения задачи состоит главным образом в обучении учащихся задавать эффективные вопросы по содержанию задач и правильно на них отвечать.
Аналитический метод можно также представить в виде системы вопросов и ответов. Для рассмотренной выше задачи эта система имеет следующий вид.
1. Что нужно знать, чтобы определить цену сукна?
Ответ: Количество купленного сукна и его стоимость.
Iа. Известно ли, сколько купили сукна?
Ответ: Да.
16. Известно ли, сколько заплатили за сукно?
Ответ: Нет.
Последний вопрос и отрицательный ответ на него дают основание задать следующий вопрос.
2. Что нужно знать, чтобы определить стоимость сукна?
Ответ: Стоимость шелка.
2а. Известна ли стоимость шелка?
Ответ: Нет.
Так как на вопрос 2а получен отрицательный ответ, то формулируется еще один вопрос.
З. Что нужно знать, чтобы определить стоимость шелка?
Ответ: Количество купленного шелка и его цену.
За. Известно ли, сколько куплено шелка?
Ответ: Да.
36. Известна ли цена шелка?
Ответ: Да.
Итак, идея решения задачи найдена.
Отметим, что количество вопросов и их содержание обусловливаются содержанием и способом решения задачи.
И основные и вспомогательные вопросы имеют вполне определенную конструкцию. Формулировать их и давать на них ответы школьники учатся в процессе решения простых задач (в данном случае — простых задач на нахождение стоимости по цене и количеству купленного, на нахождение цены по стоимости и количеству).
Синтетический метод. Синтез — логическая операция установления связи между составными частями исследуемого объекта и изучения его как единого целого. Исследуемый объект называется в требовании задачи, а его элементы описываются в условии. Сущность синтетического метода поиска решения задачи состоит в установлении связей между данными условия задачи и получении таким образом новых данных. Затем устанавливаются связи между полученными данными и так далее, до тех пор, пока не будет получено требуемое.
Поясним это на примере задачи, которая была рассмотрена выше. Условие этой задачи включает следующие данные: «куплено 4 м сукна», «куплено 14 м шелка», «за купленное сукно заплатили столько же, сколько за шелк», «цена шелка б р. за метр». Представим синтетический метод как систему вопросов и соответствующих ответов. Тогда связь между данными условия устанавливается следующим образом.
1. Что можно определить, зная, что купили 14 м шелка и цена шелка б р. за метр?
Ответ: Стоимость купленного шелка (6. 14=84).
2. Что можно определить, зная, что было куплено 4 м сукна и
14 м шелка?
Ответ: Количество купленной материи (4+14=28); на сколько больше (меньше) было куплено шелка (сукна), чем сукна (шелка)
(14—4= 10).
Очевидно, что установить какие-либо другие связи между данными условия нельзя. В то же время ни одно из полученных данных не является требуемым. Поэтому синтез продолжается: раскрываются связи между новыми данными и приведенными в условии.
3.Что можно определить, зная, что за шелк заплатили 84 р. (и что за сукно заплатили столько же)?
Ответ: Стоимость купленного сукна (84 р.).
4. Что можно определить, зная, что за 4 м сукна заплатили 84 р.?
Ответ: Цену сукна (84:4=21).
Итак, ответ получен. Заметим, что не все промежуточные результаты необходимы для решения — задача решается только в два действия. Однако, возможно, «лишние» данные пригодились бы, если бы эта задача имела другое требование.
Аналитико-синтетический метод. Рассмотрим метод, который значительно чаще, чем аналитический и синтетический, используется на практике. Он сочетает элементы и анализа и синтеза. Проиллюстрируем его на примере.
З а д а ч а 13. Школа закупила для уроков труда нитки, ткань и ножницы. За нитки уплатили 2 р., за ткань -—- 15, а за ножницы — на З р. больше, чем за нитки и ткань вместе. Сколько стоила вся покупка?
Система вопросов и ответов, отражающая процесс поиска решения задачи, может иметь следующий вид.
Анализ. 1. Что нужно знать, чтобы определить стоимость покупки?
Ответ: Стоимость ниток, ткани и ножниц.
Iа. Известна ли стоимость ниток?
Ответ: да, 2 р.
16. Известна ли стоимость ткани?

‘Ответ: да, 15 р.
Iв. Известна ли стоимость ножниц?
Ответ: Нет.
Синтез. 2. Что можно узнать из условия задачи?
Ответ: Сколько стоили нитки и ткань вместе (2+15= 17).
Синтез. 3. Что можно узнать, зная стоимость ниток и ткани?
Ответ: Стоимость ножниц (17+З20).
Итак, идея решения задачи найдена: сначала нужно найти, сколько стоят нитки и ткань вместе, затем сколько стоят ножницы и, наконец, СКОЛЬКО стоит вся покупка.
Обучение учащихся начальных классов рассмотренным методам Поиска решения задач Сводится к обучению их правильному (как минимум по форме) формулированию вопросов, соответствующих аналитическому или синтетическому методу. В старших классах обучение учащихся этим методам будет продолжено (см., например Ю. М. Колягин и др. Методика преподавания математики в средней школе.— М: Просвещение, 1975).
Основным средством обучения младших школьников приемам Поиска решения задач являются образцы рассуждений (вопросов- ответов), которые демонстрирует учитель. Вместе с тем такая работа может вестись и целенаправленно.
Уже в 1 классе учитель обращает внимание учащихся на то, что в процессе решения задачи могут формулироваться разные по форме вопросы, что форма вопроса определяет особенности ответа на него.
Пусть, например, первоклассникам предложена задача: «В вазе лежат 2 яблока и З груши. Сколько фруктов в вазе?»
Учитель формулирует вопрос, соответствующий аналитическому методу: «Что нужно знать, чтобы определить, СКОЛЬКО фруктов в вазе?» Учащиеся отвечают (возможно, с помощью учителя): «Нужно знать, СКОЛЬКО В вазе яблок и сколько груш».
Затем учитель формулирует вопрос, соответствующий синтетическому методу: «Что можно определить зная, что в вазе было 2 яблока
и З груши?» Самостоятельно ИЛИ с помощью учителя ученики приходят к следующему ответу: «Можно узнать, СКОЛЬКО всего фруктов
в вазе, или на сколько больше в вазе груш, чем яблок, или на сколько
в вазе меньше яблок, чем груш».
Затем анализируются особенности первого и второго вопросов и особенности ответов на каждый из них. Выясняется, например, что первый вопрос задается исходя из того, что спрашивается в задаче; в задаче спрашивается: «Сколько фруктов в вазе?». Значит, начиная решать задачу, мы спрашиваем: Что нужно знать, чтобы определить сколько фруктов в вазе? Чтобы ответить на этот вопрос, можно даже не знать условия задачи, причем ответ возможен только один — нужно знать, сколько в вазе фруктов каждого вида.
Второй вопрос задается исходя из того, что дано в условии задачи:
известно, что в вазе 2 яблока и З группы, значит, начиная решать задачу, мы спрашиваем: Что можно оп ред ел и т ь, з н а я, что в вазе 2 яблока и З груши? Чтобы ответить на этот вопрос, можно и не знать, что спрашивается в задаче, причем ответов может быть несколько.
Понятно, что такая работа начнет приносить плоды только при систематическом и целенаправленном ее проведении. Конечно, она потребует определенных, возможно, существенных, затрат времени, но ее полезность это оправдывает.
Существуют и другие возможности обучения методам поиска решения задач младших школьников. Они описываются в книге В. Л. Дрозда и др. «Практикум по методике начального обучения математике» (Мн., Выш. шк., 1984).
‚ Проверка решению задачи. Наиболее оперативным способом про- 4) верки решения задачи является 2л чевного учениками ответа с ответом, который сообщается учителем. Иногда, еще до того
как ученики приступили к решению задачи, учитель называет несколько ответов, из которых только один правильный. Это Оправдывается в тех случаях, когда можно предугадать, какую ошибку могут допустить учащиеся при решении данной задачи.
Задача 14. Отряд октябрят собрал 5 кг лекарственных трав, а отряд пионеров — в 4 раза больше. Сколько лекарственных трав собрали пионеры?
Если опыт решения задач такого типа (на увеличение числа в несколько раз) у учащихся невелик, то легко предугадать возможную ошибку в решении: 5+4. В самом деле, школьникам хорошо известно, как решаются задачи на увеличение числа на несколько единиц («Отряд октябрят собрал 5 кг лекарственных трав а отряд пионеров — на 4 кг больше. Сколько лекарственных трав, собрали пионеры?»). Поэтому на доске перед началом самостоятельной работы учащихся над задачей могут быть записаны два ответа: 9 кг и 30 кг,
Задача 15. С одного поля собрали9отб зерна, а с другого 2/3 этого количества. Сколько зерна собрали со второго поля?
Учитель заранее может предположить, например, что:
1) учащиеся неправильно выполнят перевод единиц массы: 90 т б ц —96 ц, тогда 96:3=32, 32. 2=64; ответ: 64 ц, или б т 4 ц;
2) учащиеся будут неправильно находить дробь числа: 906:2=
453, 453. 3=1359; ответ: 1359 ц, или 135 т 9 ц.
В таком случае одновременно с условием задачи учитель сообщает возможные ответы: 64 ц; 60 т 4 ц; 1 359 ц; б т 4 ц; 135 т 9 ц.
В начальной школе могут использоваться и другие виды проверки ‚(широко применямые учащимися в средних и стар их классах):
прикидка ответа, решение задачи1 другим способом, сопоставление / ответа и данных условия задачиф5ешение задачи, обратной данной.
Отметим, что в начальных классах учитель должен не только показать учащимся возможные способы проверки решения задачи, но и потребовать от них выполнения проверки (особенно в тех случаях, когда задача решается самостоятельно).
Прикидка ответ а — достаточно простой способ проверки решения задачи. Суть его состоит в том, что исходя из условия задачи, не выполняя, как правило, каких-либо вычислений, определяют границы, в которых должен находиться ответ.

З ад а ч а 16. В букете было несколько роз. Четыре розы подари- В букете осталось восемь роз. Сколько роз было в букете?
вполне вероятно, что некоторые учащиеся могут прийти к неправильному решению (8—4=4) исходя из того, что часть роз отдали и количество уменьшилось. Вместе с тем легко показать, что в ответе должно получиться число, большее, чем 4 и 8. Такая прикидка ответа убеждает что данная задача решается сложением.
Задача 17. Для уоков рисования купили 5 наборов карандашей и 7 наборов красок по такой же цене. За всю покупку уплатили 8 р. 40 к. Сколько стоили карандаши и сколько стоили краски?
Еще до решения задачи можно обсудить, в каких границах будут лежать искомые числовые значения. Во-первых, и стоимость карандашей, и стоимость красок меньше 8 р. 40 к. Во-вторых, карандаши
сто дешевле, чем краски. --
Вместе с тем данный способ проверки не очень надежен в самом деле, если в результате ошибок в вычислениях ученик получит ответы З р. 20 к. и 4 р. 50П, то проверка прикидкой эти ошибки не вскрыла бы.
Решение задачи другим способом обеспечивает более эффективную проверку.
За дача 18. Из двух городов навстречу друг другу одновременно выехали два автомобиля. Один ехал со скоростью 60 км в час, а другой —70 км в час. Через З ч автомобили встретились. Определить расстояние между городами.
Задача может быть решена двумя способами: 60 3+70. 3 и (60+70). 3. Получение учащимися одинаковых ответов и в первом и во втором случаях свидетельствует о том, что они верны.
Однако этот способ проверки можно использовать не всегда, так как не для ВСЯКОЙ задачи существуют разные варианты решения. Кроме того, если даже задачу можно решить несколькими способами,
то затраты времени на их поиск могут оказаться неоправданными.
В некоторых случаях для проверки решения с оп ост а в л я ют с я ответ и данные условия задачи. Обратимся к задаче 17. Предположим, что ученик получил неверный ответ: карандаши стоят З р. 20 к., а краски — 4 р. 50 к. Этот ответ Можно сопоставить с данными задачи «за всю покупку уплатили 8 р. 40 к.». В самом деле, 320+450 должно равняться 840, однако З20+450840, значит, задач решена неверно. 1
За дача 19. В двух школах 1850 учен1ов. В одной из них на 48 учеников меньше. Сколько учащихся4каждой школе?
Решая эту задачу, ученики могут использовать неверную идею:
1 850:2= 925 — СТОЛЬКО учащихся в одной школе; 925+48= 973 — во второй. В результате сопоставления полученных ответов с данными условия «в двух школах 1 850 учеников» получается, что 925+973
1 898. Значит, полученное решение неверно.
Но и этот способ можно использовать далеко не всегда. Например,
он непригоден для проверки решения задачи 12.
Наиболее эффективным, хотя и весьма трудоемким, является способ проверки решения, который состоит в р е ш е н и и з а д а

/обратной данной. /

Пусть, например, этим способом нужно проверить решение задачи

12. Для этого составляется обратная задача: полученный ответ — расстояние между городами 390 км — включается в условие задачи;

какое-либо данное условие задачи выбирается искомым, например скорость первого автомобиля; формулируется обратная задача: «Из двух городов, расстояние между которыми 390 км, навстречу друг другу одновременно выехали два автомобиля. Один из них ехал со скоростью 70 км в час. Через З ч автомобили встретились. С какой скоростью ехал другой автомобиль?» Если при решении этой задачи будет получен ответ 60 км в час, то это означает, что задача 12 решена верно.

Недостатком данного метода проверки является не только его трудоемкость. Решая задачу, обратную данной (которая, кстати говоря, иногда оказывается сложнее исходной), ученик может допустить ошибку и на основании этого предположить, что исходная задача решена неверно. А это может не соответствовать действительности.

20. ОБУЧЕНИЕ УЧАЩИХСЯ РЕШЕНИЮ ПРОСТЫХ ЗАДАЧ

Классификация простых задач. Выше был определен возможный принцип классификации простых задач: важнейшим математическим понятиям программ по математике соответствуют специальные типы простых задач.

Центральное место в программе по математике для начальных классов занимает понятие целого неотрицательного числа. Из вузовского курса математики известно, что каждое понятие характеризуется объемом и содержанием. Объем понятия целого неотрицательного числа раскрывается в начальной школе в процессе обучения учащихся счету, нумерации.

Содержание понятия целого неотрицательного числа представляется учащимся как совокупность следующих свойств: на множестве целых неотрицательных чисел выполнимы операции сложения и умножения (частично выполнимы вычитание и деление), множество целых неотрицательных чисел строго упорядочено. Это содержание раскрывается главным образом с помощью текстовых арифметических задач. Исходя из этой, так сказать, математической, точки зрения, простые задачи, решаемые в начальной школе, должны подразделяться на два класса: задачи, посредством которых у учащихся формируется представление об арифметических операциях, и задачи, которые раскрывают учащимся смысл отношений «больше», «меньше», «равно».

Однако с методической точки зрения такая классификация малоэффективна. Известно, что математические понятия усваиваются лучше, если они изучаются во взаимосвязи, сопоставляются и противопоставляются. Операции сложения и вычитания, так же как и операции умножения и деления, взаимообратны, поэтому и изучать их целесообразно во взаимосвязи. таким образом, наряду с двумя навИНЫМИ классами задач необходимо выделить задачи, раскрывающие связь между взаимнообратными арифметическими действиями И.

задачи, раскрывающие учащимся смысл отношений порядка, также должны удовлетворять определенным методическим условиям. В самом деле, в житейских ситуациях эти отношения представляются, как правило, в виде отношений «больше на (в)» и ‚<меньше на (в)$ Например, когда на практике сравниваются численности элементов двух множеств, недостаточно установитъ численность какого множества больше или меньше. Нужна более подробная характеристика: на сколько элементов больше (меньше) или во сколько раз больше (меньше). Приходится решать и обратные задачи, когда известна численность элементов одного множества, а о другом известно только, что численность его элементов на несколько единиц больше (меньше) или в несколько раз больше (Меньше).

Итак, получаем следующую систему задач, через которую раскрывается содержание понятия целого неотрицательно числа:

Ясно, что данной классификацией не исчерпываются все типы простых задач, решаемых в начальной школе. Существует еще множество понятий (в частности, нематематических, таких, как скорость, цена, урожайность и т. д.), смысл которых также раскрывается через простые задачи Однако обучение решению соответствующих задач возможно только на основе знаний о целых неотрицательных числах, поэтому методику обучения их решению мы рассмотрим в конце данного параграфа.

Простые задачи, решаемые сложением и вычитанием. Рассмотрим конкретное содержание определенной выше системы применительно к арифметическим операциям первой ступени — сложению и вычитанию. Выделим следующие типы задач:

1) задачи, раскрывающие смысл операции сложения;

2) задачи, раскрывающие смысл операции вычитания;

3) задачи, раскрывающие связь между операциями сложения и вычитания;

4) задачи, раскрывающие смысл отношений «увеличить на (несколько единиц)» и «уменьшить на (несколько единиц));

5) задачи, раскрывающие СМЫСЛ отношений «больше на» и «меньше на» (задачи на сравнение чисел с помощью вычитания, т. е. на разностное сравнение).

Аналогичным образом выделяются типы простых задач, решаемых умножением и делением:

1) задачи, раскрывающие смысл операции умножения;

2) задачи, раскрывающие смысл операции деления;

3) задачи, раскрывающие связь между умножением и делением;

4) задачи, раскрывающие смысл отношений «увеличить в несколько раз» и «уменьшить в несколько раз»;

5) задачи, раскрывающие смысл отношений «больше в... раз» и «меньше в... раз» (задачи на кратное сравнение).

Последовательность введения задач указанных типов может быть различной. Например, задачи на разностное сравнение (на кратное сравнение) могут быть рассмотрены раньше, чем задачи на увеличение (уменьшение) числа на несколько единиц (на увеличение (уменьшение) числа в несколько раз).