Вначале, очевидно, целесообразно рассмотреть процесс деления, производимый реально. К доске, например, вызываются 5 учеников. Одному из них учитель дает мешочек («корзину») с кружками («яблоками»). Предлагается раздать «яблоки» поровну остальным ученикам. Число кружков в мешочке кратно 4. Обращается внимание школьников на то, что количество «яблок», которое получит каждый ученик, неизвестно. Процесс деления «яблок» естествен
каждый ученик получает сначала по одному «яблоку», затем еще по одному и т. д.
Аналогичное задание можно предложить всем учащимся. При этом они должны использовать индивидуальные наборные полотна. Например, нужно разложить 15 «виден» на 5 «тарелок» поровну. Подводя итог этой работы, учитель показывает, как выполненную вручную операцию описать математически: 15:5=3. Вводятся термины «делимое>, «делитель», «частное».
Возможно, что целесообразно сразу же (для контраста) рассмотреть процесс деления, имеющий другой смысл. К доске вызывается ученик. Он тоже получает мешок с кружками. Ему предлагается разделить «яблоки» так, чтобы каждый ученик получил по 4 «яблока». Теперь внимание класса акцентируется на том, что неизвестно, сколько учеников получат «яблоки». Ученик у доски отсчитывает по четыре «яблока» и раздает их товарищам.
Затем организуется индивидуальная работа детей. Они должны разложить 15 «виден» по 5 в каждую «тарелку», используя наборные полотна. Учитель показывает, как выполнить соответствующую математическую запись.
В заключение полезно обсудить с учащимися общее и особенности в работе над задачами двух рассмотренных видов.
И в первой и во второй задачах дано одинаковое количество вишен (15), и эти вишни нужно разложить поровну в тарелки. Однако в первой задаче сказано, сколько всего тарелок (5). При этом неизвестно, сколько вишен окажется в каждой из них. Поэтому вишни раскладывались по одной. Во второй задаче наоборот, сообщалось, сколько вишен нужно положить в каждую тарелку (5), но спрашивалось, сколько потребуется тарелок. Чтобы ответить на этот вопрос, вишни раскладывались группами (по 5).
Такое обсуждение дает возможность еще раз уточнить смысл компонентов в полученных равенствах
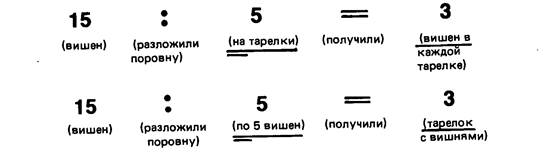
Сформированные у учащихся представления о делении закрепляются в процессе решения простых задач. Если у кого-либо из учеников возникнут затруднения, ему можно предложить проиллюстрировать решение задачи с помощью наборного полотна.
Большое значение для осознания детьми смысла деления имеют упражнения на составление задач по данным частным, причем когда по выражению нужно составить две задачи — на деление по содержанию и деление на равные части.
Задачи, раскрывающие связь между умножением и делением. Изучение операций умножения и деления во взаимосвязи обеспечивает качественное усвоение учащимися обеих операций. На практике это может достигаться разными способами.
Задачи на умножение и деление предлагаются в системе: одна задача решается умножением, а две другие, обратные ей по структуре,— делением. Задачи могут иметь разный сюжет. Например:
«Купили 4 банки с краской. В каждой банке по З кг краски. Сколько всего краски купили?»; «Купили 27 кг картофеля; он разложен поровну в 9 пакетов. Сколько картофеля в каждом пакете?»; «В магазин привезли 12 л томатного сока в двухлитровых банках. Сколько привезли банок с соком?»
Учащимся предлагается составить задачи, решаемые умножением и делением, используя, например, слова: «посадили деревья», «в каждом ряду», «всего рядов»; «принесли корзину с морковью>, «каждому кролику дали», «всего было кроликов» и т. д.
После решения задачи ученики должны проверить ее решение с помощью обратной задачи. Причем если данная задача решается делением, то обратная ей должна решаться умножением. Например, исходная задача: «для новогодних подарков купили 16 апельсинов. В каждый подарок положили по 2 апельсина. Сколько подарков приготовили к празднику?» После ее решения (получен, допустим, ответ: 4 подарка) составляется проверочная задача: «для новогодних подарков купили апельсины. Их разложили поровну в 4 подарка по 2 апельсина в каждый. Сколько всего апельсинов купили?»
Кроме перечисленных приемов (здесь перечень их неполон), используются специальные задачи, раскрывающие связь между умножением и делением. Приведем примеры таких задач.
З а д а ч а 24. для школьной столовой привезли 5 одинаковых банок с соком. Всего привезли 15 л сока. Сколько сока в каждой банке?
З а д а ч а 25. для школьной столовой привезли несколько трехлитровых банок с соком. Всего привезли 15 л сока. Сколько банок с соком привезли?
З а д а ч а 26. девять литров сока разлили поровну в банки. Всего получилось З банки с соком. Сколько сока было в каждой банке?
З а д а ч а 27. девять литров сока разлили в несколько банок поровну. В каждой банке оказалось по З л сока. Сколько всего было
банок?
З а д а ч а 28. Некоторое количество сока разлили в З банки поровну. В каждой банке оказалось по З л сока. Сколько всего было
сока?
З а д а ч а 29. Некоторое количество сока разлили по З л в каждую банку. Оказалось З банки с соком. Сколько всего было сока?
Эти задачи, так же как и задачи двух предыдущих типов, решаются либо умножением, либо делением. Однако для них характерна существенная особенность. Рассмотрим, например, задачу 24. По сюжету она напоминает задачи, с помощью которых раскрывался смысл умножения: речь идет о сумме, в которой все слагаемые одинаковы, и о значении этой суммы. Такие задачи, как известно, решаются умножением. Правда, запасать решение задачи 24 с помощью умножения удается, только используя 4ОКОШКО» или букву:

С другой стороны, эта задача решается делением 15: 5. Заметим, что «увидеть» это выражение несколько сложнее, чем уравнение. Итак, содержание задачи 24 можно выразить с помощью уравнения и с помощью выражения. Этот факт убедительно демонстрирует связь между этими операциями.
Очевидно, что решение задач 25—29 также можно выразить и уравнением и выражением. Так, задаче 25 соответствует уравнение 3-х= 15 и выражение 15:3;задачам 26 и 27 —9:х=3 и 9:3; задачам 28 и 29—х:3=3 и 3.3.
Двойственный характер задач 24—29 определяет особенности методики обучения учащихся их решению.
1. у учащихся сформированы знания и умения, необходимые для решения задач, раскрывающих смысл умножения и деления. Чтобы использовать их в полной мере, необходимо показать детям алгебраический смысл содержания задач 24_29*.
2. Поскольку операции умножения и деления используются здесь в необычных условиях, необходимо обратиться к наглядным пособиям.
3. Этим задачам соответствуют уравнения разных типов. Поэтому, вероятно, характер иллюстрации их решения будет различным.
С алгебраической точки зрения задачи 24—29 относятся к разным типам: задачи 24 и 25 — на нахождение неизвестного множителя (а. х—Ь); (х.а= Ь); 26 и 27 — на нахождение неизвестного делителя(а:х=Ь); 28и 29— на нахождение неизвестного делимого (х:а= =Ь).
Рассмотрим один из вариантов методики обучения школьников решению задач этих типов.
Задачи на нахождение неизвестного множителя. Работу над новым материалом можно начать с выполнения следующих заданий. Учащимся демонстрируется трехместный предикат, записанный на доске или выставленный в наборном полотне с помощью «окошек» и математических символов: О О = О.Составляются текстовые задачи. Сначала выбирается сюжет задачи. Затем в предикат подставляются значения множителей, соответствующие сюжету, и, наконец, формулируются условие и требование задачи.
· Иными словами, предлагается вводить понятие уравнения через задачи. Это следует из сформулированного в 18 положения, что в начальных классах любое математическое понятие должно вводиться только через текстовые задачи, такая точка зрения не совпадает с позицией авторов программы по математике для начальной школы (1986), авторов учебного пособия (<Методика преподавания математики в начальных классах М. А. Антовой и Г. В. Вельтюковой. Они полагают, что понятие уравнения должно формироваться непосредственно на основе понятий равенства и переменной. Такой подход отражен в 26 настоящего пособия.
Например, предлагается составить задач о коробках с красками. В «окошки» подставляются числа 4 и 5 5 4 = О. Имея опыт
составления задач по выражениям вида а Ь учащиеся могут сформулировать задачу: «Для урока рисования приготовили 4 коробки с красками. В каждой коробке 5 красок. Сколько всего красок в этих коробках?» Конечно, учащиеся в состоянии решить эту задачу, не обращаясь к наглядности. Однако в интересах дальнейшей работы целесообразно проиллюстрировать ее решение, например, с помощью наборного полотна: в 4 кармашка устанавливаются кружки: по 5 в каждый и т. д.
Аналогично можно составить и решить еще несколько задач. На этом подготовительная работа заканчивается.
Далее учитель создает проблемную ситуацию: он заполняет окошки» предиката необычным образом — О.]=. Спрашивается, можно ли составить задачу по этому равенству (или уравнению). После обсуждения этой проблемы составляется, например, такая задача: «В каждом ряду посажено одинаковое количество деревьев. Таких рядов — 3, всего деревьев — 15. Сколько деревьев в каждом ряду?» Здесь важно обратить внимание учащихся на очень важный момент — истолкование смысла пустого «окошка». Вполне вероятно, ученики скажут, что в каждом ряду было «неизвестное количество деревьев». В этом случае на конкретном примере
нужно пояснить, что, поскольку рассматривается операция умножения, слагаемые должны быть одинаковыми. Поэтому хоть и неизвестно, сколько деревьев в каждом ряду, но их там поровну.
Чтобы решить данную задачу, учащиеся под руководством учителя выполняют практическую работу с иллюстративным материалом. Она может сопровождаться следующим комментарием: «Известно, что было три ряда деревьев. Значит, на наборном полотне придется использовать три кармашка. Всего было 15 деревьев. Отсчитаем 15 кружков.. В задаче не сказано, сколько деревьев в каждом ряду, но известно, что в каждом было одинаковое количество. Поэтому 15 кружков нужно разложить поровну в каждый из трех кармашков». Учащиеся знают, как поступить в таком случае: 15 кружков раскладывают по одному в кармашек. Знают они, и как описывается этот процесс математически — 15:3=5.
В заключение констатируется, что зависать решение данной задачи можно двумя способами: О. 3= 15 или 15:3. Первая запись называется уравнением. Оно может быть записано иначе — х. 3= 15. Формулируется правило его решения.
Ясно, что методика работы над задачами, которым соответствует уравнение а. х = Ь, не имеет принципиальных особенностей.
Задачи на нахождение неизвестного делителя. План обучения учащихся решению задач этого типа может быть таким же, как и задач на нахождение неизвестного множителя. Сначала ученики составляют и решают задачи известного им типа, которые раскрывают смысл операции деления. Затем учитель предлагает составить задачу по необычной записи:: х =, где а, ЬЛТ и аЬ. С помощью наборного полотна демонстрируется процесс предматематического решения задачи нового типа. И, наконец, это решение описывается математически. Остановимся- на содержании практической работы учащихся с наборным полотном, выполняемой под руководством учителя.
Пусть по предложенному учителем уравнению 15: 0=3 детьми составлена такая задача: «Всего было 15 карандашей. Их разложили в несколько коробок. В каждой оказалось по З карандаша. Сколько было коробок с карандашами?»
В соответствии с условием задачи учащиеся отсчитывают 15 кружков и раскладывают их группами по З в кармашки наборного полотна. Такая операция выполнялась при решении задач, раскрывающих смысл деления по содержанию. Поэтому предматематическое решение описывается частным 15:3.
По уравнению 15:0=3 целесообразно составить и другую задачу: «Всего было 15 карандашей. Их разложили поровну в коробки. Получилось З коробки с карандашами. Сколько карандашей положили в каждую коробку?» Выполняется практическая работа, сопровождающаяся, например, таким комментарием: «Известно, что всего было 15 карандашей. Отсчитаем 15 кружков. Карандаши разложили в З коробки. Значит, приготовим З кармашка наборного полотна.. Карандаши разложили в коробки поровну, поэтому раскладываем кружки по одному в каждый кармашек. Таким образом, 15 разделим на З равные части — 15:3=5».
Задачи на нахождение неизвестного делимого. При обучении решению таких задач основные элементы рассмотренной выше методики остаются неизменными. Разница состоит, в частности, в том, что задачи составляются по уравнению 0:5=3, например: «Несколько плодовых кустов посадили по 5 кустов в ряд. Всего оказалось З ряда кустов. Сколько кустов посадили?» «Несколько плодовых кустов посадили в 5 рядов. В каждом ряду — по З куста. Сколько кустов посадили?»
Предматематическое решение первой задачи может комментироваться так: «Сколько всего кружков нужно разложить по кармашкам, неизвестно, но в каждом должно быть по 5 кружков. Причем кружками заполняются З кармашка. Чтобы посчитать, сколько всего кружков в наборном полотне, нужно 5 умножить на 3».
В заключение подчеркнем, что главным в обучении учеников решению задач, раскрывающих связь между умножением и делением, являются предметные иллюстрации, отражающие взаимосвязанность этих операций. При желании учитель может использовать возможность обучения детей решению уравнений. В таком случае важная роль отводится заданиям на составление задач по данному уран- нению.
Задачи на увеличение (уменьшение) числа в несколько раз. Приступая к решению задач данного типа, учащиеся часто смешивают их задачами на увеличение (уменьшение) числа на несколько единиц. Это, пожалуй, единственная серьезная проблема, с которой сталкивается учитель. Поэтому методика должна быть ориентирована на противопоставление задач этих двух схожих типов. Например, учащимся могут быть предложены одновременно две задачи: «У Сережи 4 карандаша, а у Наташи на З карандаша больше. Сколько карандашей у Наташи?»; «У Сережи 4 карандаша, а у Наташи в З раза больше. Сколько карандашей у Наташи?» Еще при ознакомлении учащихся с текстами этих задач учитель предлагает сравнить их условия и требования. Ученики, вероятно, отметят, что числовые данные в условиях обеих задач одинаковы: — 4 и 3; однако в первой задаче число З означает количество карандашей, во второй — «число раз»; в первой задаче сказано «на 3», а во второй — «в З раза»; вопросы в задачах одинаковы.
Учитель кратко записывает условия этих задач, выделяя существенные элементы:
Сережа — 4 карандаша Сережа — 4 карандаша
Наташа —? на З карандаша Наташа —? в З раза больше
Наконец, для каждой задачи выполняются иллюст5ации, например, с помощью наборного полотна. Содержание первой задачи ученики могут проиллюстрировать самостоятельно, для них не должно составлять труда и решение этой задачи, для второй задачи иллюстрацию выполняет учитель (рис. 58). Она служит основой

поиска решения: у Сережи 4 карандаша, а у Наташи «3 раза по столько», значит, у Наташи 12 карандашей (4 ‘3).
Закрепляя навыки решения задач нового типа, полезно чередовать их с задачами на увеличение числа на несколько единиц, упражнять учеников в составлении задач этих двух типов (по выражениям а.Ь и а+Ь), Можно предлагать и задания, например, такого типа: «догадайся, какие слова нужно вставить вместо точек. Составь задачу и реши ее»:
1) рост Сережи в 5 лет —9 дм;
рост Сережи в 7 лет —?... 2... больше.
2) зима — З месяца;
год —?... 4... больше.
Таким же образом ученики знакомятся с решением задач на уменьшение числа в несколько раз, т. е. сначала сравниваются тексты и кратко записанные условия этих задач и задач на уменьшение числа на несколько единиц; содержание задач иллюстрируется и описывается на математическом языке; выполняются упражнения на закрепление.
Задачи на сравнение чисел с помощью операции деления (задачи на кратное сравнение). При обучении учеников решению задач данного типа за основу может быть взят методический подход, рассмотренный выше.
Наиболее распространенной ошибкой, которую допускают ученики, является решение задач на кратное сравнение вычитанием, т. е. решение их как задач на разностное сравнение. Для того чтобы предупредить ее, следует с самого начала противопоставить такие задачи. С этой целью ученикам одновременно предлагаются задачи одного и другого типов, выясняется, чем похожи и чем различаются их условия и требования.
Пусть, например, рассматриваются такие задачи: «К кормушке прилетели 8 снегирей и 2 синицы. На сколько снегирей больше, чем синиц?»; К кормушке прилетели 8 снегирей и 2 синицы. Во сколько раз снегирей больше, чем синиц?» Дети наверняка заметят, что в этих задачах одинаковые условия. Различаются только требования:
в первой задаче спрашивается «на сколько», а во второй «во сколько раз». Эту особенность можно подчеркнуть при краткой записи содержания задач.
Следующий этап работа с иллюстративным материалом. Она имеет особое значение при решении задач на кратное сравнение. Весьма вероятно, что умение решать задачи на увеличение числа в несколько раз некоторые ученики могут попытаться использовать в новой ситуации, рассуждая, например, так: «Чтобы увеличить число в несколько раз, нужно выполнить умножение. В задаче о снегирях и синицах говорится: «во сколько раз больше», значит, эта задача решается умножением».
На наборном полотне выполняется иллюстрация для первой задачи. Ученики делают это самостоятельно. Известным образом эта иллюстрация преобразуется, и записывается соответствующее математическое выражение: 8—2. Иллюстрацию ко второй задаче предлагает учитель (рис. 59). «Чтобы ответить на вопрос, во сколько
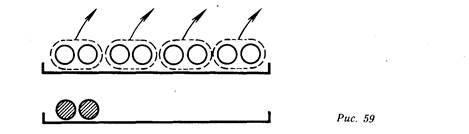
раз снегирей больше, чем синиц,— объясняет учитель,— нужно определить, сколько раз по 2 содержится в 8». Получить ответ на вопрос задачи можно и практически убирать кружки, обозначающие снегирей, по два и затем посчитать, сколько раз это удалось сделать. Учащимся известно, что на языке математики это означает: 8:2=4.
В заключение подчеркивается, что, решив данную задачу, получили и ответ на вопрос: во сколько раз синиц меньше, чем снегирей.
Выше был рассмотрен лишь один из возможных вариантов методики обучения учащихся решению задач на кратное сравнение. Вероятно, изучение этой темы можно было бы начать с рассмотрения задачи, обратной задаче на увеличение (уменьшение) числа е несколько раз. Однако в любом случае роль иллюстраций является определяющей.
Другие важнейшие типы простых задач. Традиционным для программы по математике для начальных классов являются понятия д о л и и д р о б и. Не исключение и программа 1986 г. Необходимость знакомства младших школьников с этими понятиями естественна, поскольку с операцией деления предметов, множеств предметов и величин на равные части, со словами «половина», «треть», «четверть» дети часто сталкиваются в быту. Важная роль в формировании представлений о доле и дроби принадлежит текстовым задачам.
Из вузовского курса математики известно, что понятие дроби связано с расширением кольца целых положительных чисел до поля положительных рациональных чисел. Рассматривались два подхода к такому расширению аксиоматический и на основе измерения длины отрезка. Положительным рациональными числом назывался класс эквивалентных упорядоченных пар натуральных чисел или класс эквивалентных дробей. На множестве определялись операции, доказывались их Свойства.
Программой 1986 г. не предусмотрено изучение младшими школьниками операций на множестве обыкновенных дробей, поэтому формирование у них представлений о дроби как о числе невозможно. Первоначальные Сведения о дробях учащиеся должны получить через практические действия над реальными объектами, геометрическими фигурами, величинами Таким образом, методическая проблема знакомства учащихся с дробями состоит в выборе учителем целесообразного множества исходных объектов и практических операций, которые ученики будут выполнять над ними. Понятие дроби будет отождествляться с результатом этой операции.
Для решения этой проблемы можно воспользоваться определением рационального числа через измерение длины отрезков. (Конечно, не подходом в целом, а лишь некоторыми его элементами.)
Начнем с содержания практической процедуры, результат которой дети будут математически описывать обыкновенной дробью. Она имеет много общего (но не совпадает) с процессом измерения длины отрезка. Если некоторый объект А удается разделить на Ь равных частей и взять а таких частей, то результат этой операции можно выразить так: получена -- часть объекта А. Допустим, А характеризуется каким-либо свойством, например длиной, которое выражается числом п(А). Тогда результат описанной операции над А выразится числом С = п(А):Ь. а. Это число показывает, какую длину имеет
часть объекта А. Такое представление о дроби имеет ряд существенных особенностей. Например, с точки зрения ученика, символ не имеет Смысла, так как непонятно, что именно разделено на 4 равные части. У выражения «{. яблока» или «- отрезка АВ>? смысл есть: яблоко или отрезок АВ разделены на 4 равные части, и взята одна такая часть. Как следствие, учащиеся не смогут осознанно
ответить на вопрос: какая из дробей больше: 4- или —-. Такие ВООСЫ в начальных классах вообще некорректны. Пытаясь ответить на них, ученики могут прийти к удивительным «открытиям», которые негативно повлияют на усвоение соответствующего материала в средних классах. Например, дети могут «установить», что 4-.с-- (ведь половина яблока меньше трети арбуза!) или что
(если сравниваются доли сливы и яблока). другое дело, если вопрос формулируется так: «Что больше: 4- или 4- отрезка АВ?»;
«Что больше: -- или 4- яблока?» и т. д. Сравнение чисел, представленных в виде дроби, возможно только в У классе, после того как определится их место на числовом лучё, выяснится смысл арифметических операций на множестве таких чисел.
дидактически нецелесообразно также рассматривать с учащимися неправильные дроби. Их смысл может показаться детям загадочным. Например, 4 отрезка АВ означает, что этот отрезок разделили на З равные части и взяли 4 такие части. Непонятно, откуда взялась четвертая часть!
Рассмотренная выше операция определяется на множестве объектов, которые учащиеся младшего возраста способны разделить на равные части. Это любые предметы, которые можно изобразить в виде геометрических фигур, «хорошо» делящихся на равные части практически,— отрезков, прямоугольников, квадратов, кругов.
Процедура получения - части А состоит из двух операций —деления А на Ь равных частей и получения а таких частей. Поэтому формирование у учеников понятия дроби начинается с изучения долей.
Изучение темы «доли» можно предварить беседой. Учитель и ученики проводят примеры житейских ситуаций, связанных с практическим делением предметов на равные части. Например, два друга разделили пополам яблоко; 4 одноклассника разделили между собой поровну плитку шоколада и т. д.
Затем организуется практическая работа с вырезанными из бумаги геометрическими фигурами (равносторонними и равнобедренными треугольниками, прямоугольниками и квадратами, равнобедренными трапециями, кругами, моделями отрезков). Соответствующие фигуры имеет каждый ученик. Под руководством учителя дети делят эти фигуры на заданное количество равных частей путем перегибания. Эта работа будет носить творческий характер, если наряду с названными фигурами у учащихся будут и такие, которые разделить на равные части перегибанием невозможно (рис. 60). Выполнение этих заданий способствует пониманию
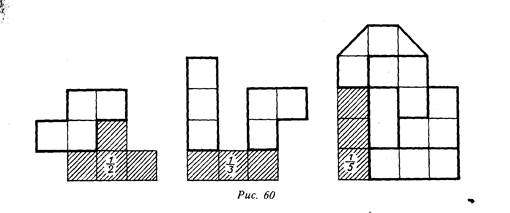
(на интуитивном уровне, конечно) того, что получить -..- долю фигуры
можно не только делением этой фигуры на равные, но и на равно- великие части.
В процессе такой работы уточняется смысл терминов «половина», «треть», «четверть». Здесь же разъясняется смысл записей:
Практически решаются и обратные задачи: «Покажи 4- круга, 4- квадрата, 4- отрезка» и т. д. Выполняемые операции комментируются.
Принципиально новым этапом при знакомстве с понятием доли является работа над получением 4-, 4-, 4, 4- долей фигуры. В
самом деле, далеко не всякую фигуру можно разделить на п равных частей перегибанием, если не является степенью 2. для простоты достаточно ограничиться рассмотрением отрезков.
Сначала учеников полезно поупражнять в делении отрезка на З, 5, 6 равных частей «на глаз» с последующей проверкой результата путем перегибания модели. Не лишне показать учащимся, как разделить отрезок на равные части с помощью циркуля (необходимый раствор циркуля подбирается методом проб). Таким образом, они убеждаются, что деление отрезка на равные части иногда совсем не простое дело. Поэтому учеников необходимо ознакомить с другим способом деления отрезка на равные части. Суть его в том, что делится не сам отрезок, а число, которое получается в результате измерения этого отрезка. К такому выводу учеников можно подвести, например, следующим образом. Им предлагается начертить в тетради отрезок длиной 12 клеток, а затем разделить его на 2, 3, 4, 6 и 12 равных частей; отрезок длиной 15 клеток и разделить его на 3, 5, 15 равных частей; прямоугольник со сторонами б и 15 клеток и разделить его на 3, 4, 5 равных частей. Последнее, самое сложное, задание выполняется следующим образом. Учащиеся замечают, что ни одна из сторон не делится на 4 равные части нацело. Поэтому подсчитывается общее количество клеток в прямоугольнике 15. 6. (Хотя с понятием площади и правилом вычисления площади прямоугольника ученики еще не знакомы, догадаться, как проще пересчитать клетки в данном прямоугольнике, не очень сложная задача.) Полученный результат — 80 — делится на 4. Значит,
4- прямоугольника состоит из 20 клеток. Ответ проверяется практически.
Наконец, учащиеся учатся решать текстовые задачи, в которых используется понятие доли.
Практическая работа на предыдущих этапах сводилась к определению доли какой-либо геометрической фигуры или числа, выражающего длину отрезка. Поэтому школьники уже подготовлены к решению задач на нахождение доли числа: (1) <В бригаде 84 рабочих. Комсомольцы Составляют -- всех членов бригады. Сколько
комсомольцев в бригаде?»
Понятно, что представления о доле будут у учащихся более глубокими, если наряду с задачами этого типа будут решаться обратные задачи. Для задачи (1) можно составить две обратные:
(2) <В бригаде 28 комсомольцев. Они составляют.- всех членов бригады. Сколько рабочих в бригаде?»; (3) «В бригаде 84 рабочих.
Среди них 28 комсомольцев. Какую долю рабочих составляют
КОМСОМОЛЬЦЫ?»
Чтобы при решении этих задач ученики могли использовать имеющиеся у них знания, учитель должен показать, как перевести их содержание на язык геометрических фигур. Используется методика работы по образцу: учитель с пояснениями выполняет чертежи в соответствии с условиями задач, учащиеся воспроизводят их у себя в тетрадях. Таким образом учащиеся приобретают опыт иллюстрации задач с помощью чертежей. Это позволит им в дальнейшем выполнять такую работу самостоятельно.
Поиск решения задачи (1) осуществляется, например, следующим образом. Строится отрезок АВ, обозначающий количество всех рабочих бригады (рис. 61, а). Комсомольцы, по условию задачи, составляют 1/3 всех рабочих, поэтому АВ делится на З равные части. Отрезок АС соответствует количеству комсомольцев; АВ — количеству членов бригады (84), значит, отрезку АС соответствует 84:3, или 28 человек.
План решения задачи (2) также вырабатывается в процессе построения чертежа (рис. 61, 6). Пусть количеству комсомольцев соответствует отрезок АС. Тогда отрезок, соответствующий количеству всех рабочих бригады (АВ), будет в З раза больше АС. Значит, всего в бригаде 28. 3, или 84 рабочих.
Выполняя чертеж к задаче (3), учитель конкретизирует требование задачи: если исходный отрезок АВ (рис. 61, в) соответствует 84 рабочим, то каким по длине будет отрезок АС, соответствующий количество комсомольцев (т. е. где на отрезке АВ поставить точку С)? Это определяется арифметически — 84:28=3. Число З показывает,
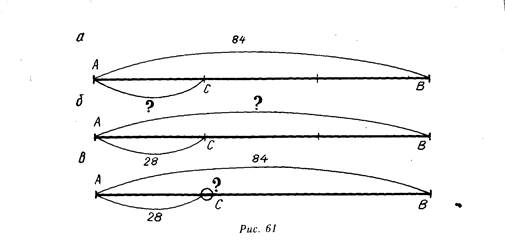
сколько раз по 28 содержится в числе 84. Значит АВ нужно разделить на З равные части. Одна из них и соответствует количеству комсомольцев в бригаде. При делении отрезка на равные части получаются, как известно, доли этого отрезка. В данном случае
Это и есть ответ на вопрос задачи.
Достаточно подробное обсуждение вопросов, связанных с понятиями доли и дроби, избавляет нас от необходимости останавливаться на методике изучения дробей в начальной школе. Отметим лишь, что программой предусмотрено обучение учащихся решению задач только одного типа -— на нахождение дроби числа.
Понятие функция является одним из фундаментальных математических понятий. Большое внимание его формированию уделяется в курсе математики средней школы, В младших классах возможности для формирования у учащихся представлений о функциональных зависимостях весьма ограничены. Однако такие возможности есть, и учитель обязан их использовать.
/ Одними из простейших видов функциональных отношений явля4тся прямая и обратная пропорциональные зависимости. Из вузовского курса математики известно, что если одна из трех величин равна частному двух других и ее значения постоянны, то значения двух других меняются прямо пропорционально. Если же одна из трех величин равна произведению двух других и ее значения постоянны, •то две другие величины связаны обратно пропорциональной зависимостью.
 2015-07-14
2015-07-14 1139
1139
