УIII. Величины и их измерение 31. Величины в начальнои школе

Понятие величины широко применяется не только в математике, но и в физике, химии, биологии, астрономии и других науках. В школе это понятие используется не всегда корректно: считаются синонимами термины «величина» и «количество», смешивают термины «величина» и «значение величины», говорят о «величине величины», когда, например, для характеристики площади фигуры применяют словосочетание «величина площади» и т. д.
Объясняется это тем, что понятие величины не является чисто математическим. Применение его во многих отраслях науки привело к разночтению, употреблению его в различных смыслах. В методике начального обучения математике понятие величины долгое время связывали с понятием «именованное число»*. Причем считали, что понятие величины уже известно из повседневной жизни, а его свойства очевидны. В курсе методики преподавания математики ограничивались указанием наиболее характерных упражнений для различных классов величин. Это приводило к смешению понятия величины с понятием меры (числа, выражающего величину после выбора некоторой единицы измерения).
В естественных науках под величинами понимают определенные свойства физических тел. Некоторые величины (длину, площадь, объем, массу, время, скорость, цену, стоимость) изучают в курсе математики начальной школы.
В математике на вопрос «Что такое величина?» ответа в виде определения («величиной называется...») нет. Однако с помощью исходных свойств, характеризующих величины, строится вся теория величин. Рассмотрим систему упражнений, конкретизирующих некоторые свойства величин, доступные учащимся начальной школы. В первом классе отрезки сравниваются наложением. Это приводит к понятию длины: два отрезка имеют одну и ту же длину, если
один совпадает с другим при наложении; если же какой-то из сравниваемых отрезков накладывается на часть другого, не покрывая
его целиком, то длина первого отрезка меньше длины второго. Обнаруженное учащимися в ходе практических работ свойство длин отрезков, полосок бумаги, ленточек, туго натянутых нитей, проволочек обобщается: в множестве отрезков устанавливается отношение порядка (либо длины отрезков совпадают, либо первый отрезок меньше второго, либо второй отрезок меньше первого). длины отрезков можно складывать (если точка В лежит между точками А и С, то длина отрезка АС равна сумме длин отрезков АВ и ВС (рис. 81)).
* Этот не очень удачный термин применяется в методике обучения математике в начальной школе в настоящее время. В данном пособии мы пользовались им, отдавая дань традиции.

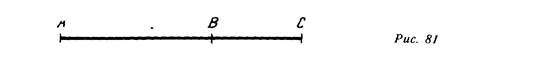
Смысл отношения «меньше» и операции сложения натуральных чисел поясняется на примере различных конкретных величин.

Приведем систему упражнений, раскрывающих некоторые свойства понятия длины отрезка.

1. Упражнения, иллюстрирующие упорядоченность множества отрезков отношением «иметь меньшую длину>.

1. Сравните красный и синий отрезки. Какой отрезок короче? Верно ли, что красный отрезок длиннее синего; синий отрезок длиннее красного? (Это упражнение иллюстрирует свойство асимметричности отношения «меньше.)

2. Сравни красный, синий и зеленый отрезки. Назови самый короткий, самый длинный отрезок. Что можно сказать о третьем от- резке относительно самого длинного? Свойство транзитивности отношения «меньше» раскрывается. при выполнении следующих заданий.

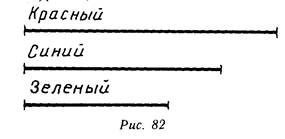
Сравни по длине зеленый и синий отрезки, (Зеленый отрезок короче синего.) Сравни синий и красный отрезки. (Синий отрезок короче красного.) Сравни длины зеленого и красного отрезков. (Зеленый отрезок короче красного.

Почему?) Если по длине зеленый отрезок меньше синего, а синий меньше красного, то длина зеленого отрезка меньше длины красного — подводит итог сравнения длин отрезков учитель (рис. 82).

II. Упражнения, приводящие к понятию длины отрезка.

1. Определите длину каждого отрезка (рис. 83).

2. Вычислите, на сколько сантиметров длина первого отрезка меньше длины второго отрезка.

iii. Упражнения, иллюстрирующие переместительное свойство сложения длин отрезков.

Расстояние от Москвы до Свердловска 1667 км, а от Свердловска до Новосибирска 1524 км. Чему равно расстояние от Москвы до Новосибирска? Чему равно расстояние от Новосибирска до Москвы?

При решении этой задачи составляются такие выражения:

1667+ 1524 (км) — расстояние от Москвы до Новосибирска;

1524+ 1667 (км) —расстояние от Новосибирска до Москвы.

Решение этой задачи подтверждает свойство переместительности сложения в множестве длин отрезков. IУ. Упражнения, иллюстрирующие сочетательное свойство сложения длин отрезков.

Расстояние от Москвы до Свердловска 1667 км, от Свердловска до Новосибирска 1524 и от Новосибирска до Иркутстка 1851 км. Чему равно расстояние от Москвы до Иркутска?

При решении этой задачи следует составить такие математические выражения:

(1667+1524)+1851 (км) —расстояние от Москвы до

Иркутска;

1667+(1524+1851) (км) —расстояние от Москвы до

Иркутска.

Вычисляя значения этих выражений, учащиеся устанавливают, что сложение величин ассоциативно.

У. Задания, иллюстрирующие свойство монотонности сложений в множестве длин отрезков.

От села Сосновка до села Красное 24 км, а от села Красное до

села дачное 18 км. Сравнить расстояние от Сосновки до Красного

с расстоянием от Сосновки до дачного (рис. 84). 14 по чертежу, и

по условию задачи учащиеся устанавливают, что 24 24 + 18. УI. Задачи, неявно вводящие следующее свойство длины отрезка:

длину отрезка можно делить на любое число п одинаковых частей. Начертите отрезок длиной 12 см и разделите его на З равные ча-

сти, а затем каждую из них на 2 равные части. На сколько равных частей можно разделить весь отрезок? Чему равна длина шестой

части данного отрезка?

По такому же принципу может быть построена система упражнений для введения понятия площади геометрической фигуры.

1. Площадь какой из фигур, изображенных на рис. 85, меньше? Верно ли, что площадь круга меньше площади квадрата? (Свойство асимметричности отношения «меньше» на множестве площадей геометрических фигур.)

Верно ли, что площадь данного прямоугольника меньше площади этого же прямоугольника? (Свойство антирефлексивности отношения «меньше на множестве площадей геометрических фигур.)

Сравните площади фигур (рис. 86).

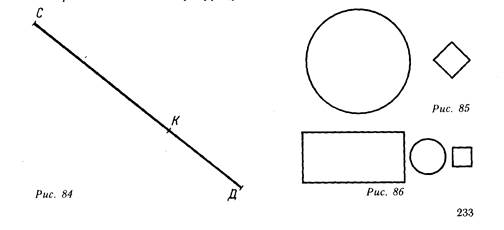
Наложением фигур друг на друга дети устанавливают, что площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника Учащиеся убеждаются также, что площадь квадрата меньше площади прямоугольника. Учитель подводит итог этой работы: Так как площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника, то площадь квадрата меньше площади Прямоугольника».

II. На сколько квадратных сантиметров площадь квадрата со стороной З см меньше площади квадрата со стороной 5 ем? (Существование разности площадей.)

УI. Измерение площади фигуры с помощью палетки свидетельствует о том, что любую площадь можно делить на несколько одинаковых частей.

УII. Измерить площадь обложки учебника «Математиках’ в квадратных дециметрах и квадратных сантиметрах. Сравнить результаты измерения.

Учащиеся убеждаются, что площадь обложки удобнее измерять в квадратных сантиметрах. Они устанавливают практически, что

площадь обложки учебника меньше 4 квадратных дециметров и равна 352 (22. 16) квадратным сантиметрам.

Выше была рассмотрена методика введения двух величин — длины и площади. Общими для процесса введения понятия величины являются следующие этапы.

(1. Задается некоторое множество А, которое является областью определения величины.

2. Из данного рода величин выбирается некоторая величина (е) которую называют единицей измерения.

3. Осуществляется процесс измерения — сравнения данной величины с выбранной единицей измерения, результатом которого является некоторое значение величины.

Изучение величин в курсе математики начальной школы имеет прIiюй4Р. Учащиеся знакомятся с непосредственным измерением длин отрезков, определяют вместимость сосудов, массу тел, температуру воздуха, учатся определять время по часам, даты по календарю, площадь фигуры с помощью палетки.

Ученики, оканчивающие начальную школу, должны знать, что на множестве изученных величин (длина, площадь, вместимость, масса, время) определены отношения равенства и неравенства.

Они устанавливаются как практики (непосредственно), таки косвенно. Все величины можно йзiщр1ть, причем для каждой из них есть свой способ измерения, сущность которого заключается в сравнении данного объекта с единицей его измерения. Величины одного и того же рода можно скаць и вычитать; умножать и делить на отвлеченные числа; находить часть величины. Между величинами одного и того же рода существует определенная зависимость, знание которой необходимо для выполнения преобразований величин: выражения одной и той же величины в различных единицах измерения.

Обучение измерению разных величин строится по одной и той же схеме.

1. Производится сравнение величин «на глаз», с помощью мускульных усилий.

2. Вводятся единицы измерения величины и устанавливаются отношения между ними и ранее рассмотренными.

3. Величины преобразуются: крупные заменяются мелкими, а мелкие — крупными.

4. Величины сравниваются путем измерения.

5. Производятся операции над величинами.

Величины изучаются в тесной связи с арифметическим и геометрическим материалом. Они иллюстрируют отношения, свойства арифметических операций на множестве натуральных чисел и обыкновенных дробей. Преобразования величин связаны с изучением нумерации натуральных чисел.

Геометрические фигуры служат средством наглядности изучения величин и измерения.