| Элемент модели | 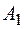
| 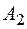
| 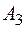
| 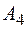
| 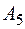
| 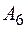
|
| Вероятность возникновения риска | 0,1 | 0,2 | 0,3 | 0,1 | 0,1 | 0,1 |
| Ущерб (потери) при возникновении риска |
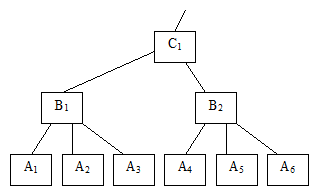
В соответствии с формулами получим следующие вероятности рисковых событий по уровням декомпозиции модели
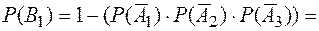
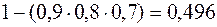 ;
;
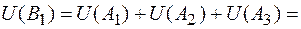
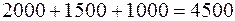 ;
;
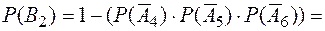
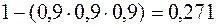 ;
;
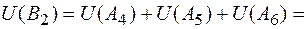
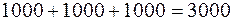 ;
;
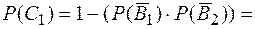
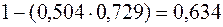 ;
;
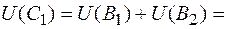
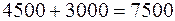 .
.
Это дает возможность предварительно оценить потенциально возможный риск проекта до начала его реализации. Для рассмотренного примера вероятность возникновения неблагоприятного события 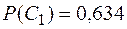 , максимально возможный ущерб составит
, максимально возможный ущерб составит 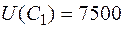 .
.
Для более точных оценок рисков проекта в ходе его реализации можно использовать формулу полной вероятности
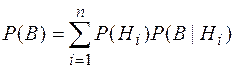 ,
,
где 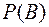 – вероятность события
– вероятность события 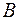 ;
;
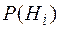 – вероятности гипотез относительно события
– вероятности гипотез относительно события 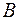 ;
;
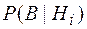 – условная вероятность события
– условная вероятность события 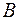 при этой гипотезе.
при этой гипотезе.
Для рассматриваемого примера риск на элементе 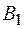 может появиться при следующих гипотезах:
может появиться при следующих гипотезах:
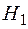 - риск возникнет только на элементе
- риск возникнет только на элементе 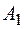 ;
;
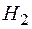 - риск возникнет только на элементе
- риск возникнет только на элементе 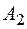 ;
;
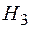 - риск возникнет только на элементе
- риск возникнет только на элементе 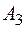 ;
;
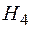 - риск возникнет только на элементах
- риск возникнет только на элементах 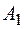 и
и 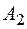 ;
;
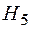 - риск возникнет только на элементах
- риск возникнет только на элементах 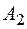 и
и 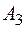 ;
;
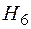 - риск возникнет только на элементах
- риск возникнет только на элементах 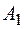 и
и 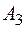 ;
;
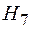 - риск возникнет только на элементах
- риск возникнет только на элементах 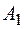 ,
, 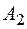 и
и 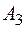 ;
;
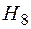 - риск не возникнет ни на одном элементах
- риск не возникнет ни на одном элементах 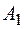 ,
, 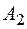 и
и 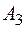 ;
;
Предположим, что событие 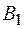 (риск) появиться, если верны гипотезы
(риск) появиться, если верны гипотезы 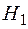 ,
, 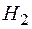 ,
, 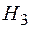 ,
, 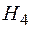 ,
, 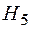 ,
, 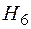 ,
, 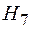 , то есть условные вероятности равны:
, то есть условные вероятности равны:
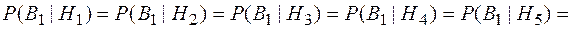
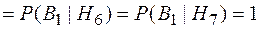 ;
; 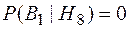 .
.
Теперь определим вероятности гипотез:
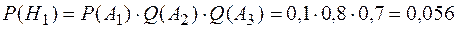 ;
;
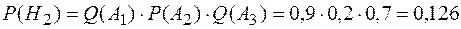 ;
;
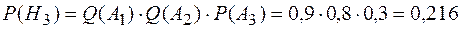 ;
;
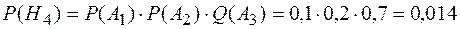 ;
;
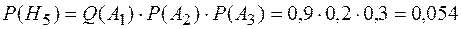 ;
;
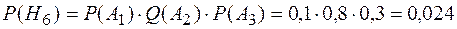 ;
;
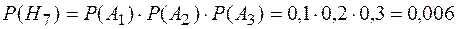 ;
;
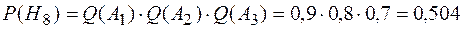 .
.
Тогда вероятность возникновения риска на элементе 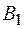 будет
будет
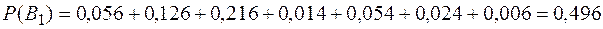 .
.
После определим ущерб (потери) для данных гипотез:
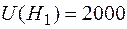 ;
;
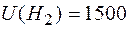 ;
;
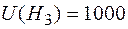 ;
;
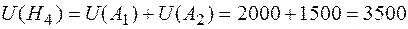 ;
;
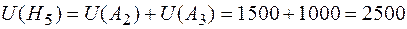 ;
;
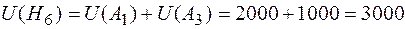 ;
;
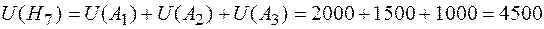 ;
;
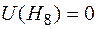 .
.
Таким образом, вероятность максимального ущерба на элементе 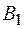 (
(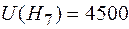 ) равна
) равна 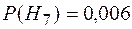 .
.
Для данной ситуации, если в качестве ущерба на элементе 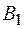 принять математическое ожидание потерь при условии реализации гипотез
принять математическое ожидание потерь при условии реализации гипотез 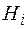 , то большое влияние на результат окажет вероятность не возникновения риска ни на одном элементах
, то большое влияние на результат окажет вероятность не возникновения риска ни на одном элементах 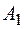 ,
, 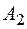 и
и 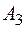 (
(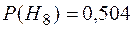 ). Поэтому для оценки средней величины ущерба (потерь) необходимо предположить, что риск на элементе
). Поэтому для оценки средней величины ущерба (потерь) необходимо предположить, что риск на элементе 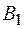 возникнет.
возникнет.
В случае возникновения рискового события можно пересчитывать вероятности гипотез, используя формулу Байеса.
Для рассматриваемого примера допустим, что рисковое событие наступило на элементе 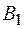 . Тогда апостериорные вероятности гипотез будут следующими:
. Тогда апостериорные вероятности гипотез будут следующими:
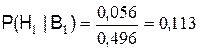 ;
;
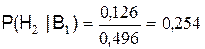 ;
;
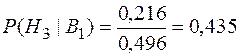 ;
;
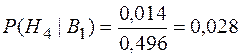 ;
;
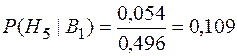 ;
;
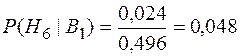 ;
;
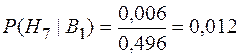 ;
;
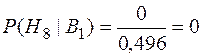 .
.
Используя формулу полного математического ожидания, получим среднюю величину ущерба (потерь):
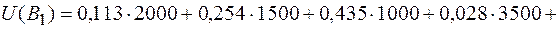
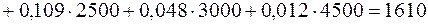 .
.
Аналогично определяем вероятность возникновения риска на элементе 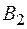 , апостериорные вероятности гипотез, среднюю величину ущерба (потерь):
, апостериорные вероятности гипотез, среднюю величину ущерба (потерь):
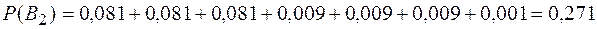 .
.
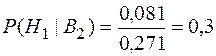 ;
;
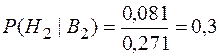 ;
;
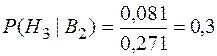 ;
;
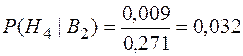 ;
;
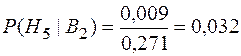 ;
;
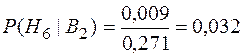 ;
;
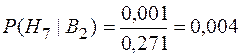 ;
;
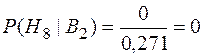 .
.
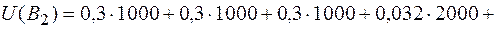
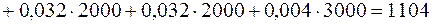 .
.
Подобным образом определяем вероятность возникновения риска на элементе 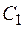 , апостериорные вероятности гипотез, среднюю величину ущерба (потерь):
, апостериорные вероятности гипотез, среднюю величину ущерба (потерь):
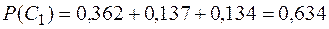 .
.
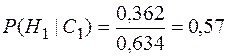 ;
;
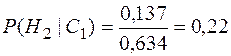 ;
;
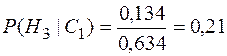 ;
;
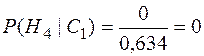 .
.
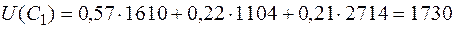 .
.
 2015-07-14
2015-07-14 365
365







