2015-07-14
663
В логическом подходе обработки знаний осуществляется представление знаний в виде суждений. Составными частями суждений являются объект суждения, предикаты и логические связки.
В двухзначной логике Буля характер связи между объектом и субъектом суждения не устанавливается.
Польский математик Ян Лукасевич впервые предложил устанавливать такой характер связи через модальные операторы:
1. (х) – необходимо х
2. ◊(х) – возможно х
3. 
(х) – случайно х
Назначение модальных операторов заключается в определении значения функции, зависящей от модальности.
| И |
| Л |
| I |
| P |
| И |
| необходимая И |
| возможная И Л |
| необходимая Л |
Рис. 28.
Исходные два класса семантических значений И и Л Лукасевич разбил на подклассы: необходимость и возможность, при этом подклассы необходимость И и Л рассматриваются приемники семантических значений И и Л. Подклассы возможных состояний не являются самостоятельными. Их объединяют в 2 класса случайных событий.
Таким образом семантика любой переменной определяется 3 значениями:
0 – возможность
1 – необходимость
2 – случайность
| 
|
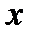
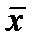
Рассмотрим основные и вспомогательные модальные операции.
|
|
| 
| 
| 
|
| 
| 
|
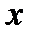
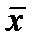
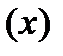
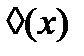
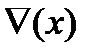
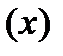
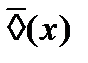
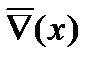
| основные |
| вспомогательные |
Рис. 29.
Модальный оператор – двузначная функция, определяющая своим первым значением соответствующий ей модальный знак.
Установим связь между модальными операциями прямого значения х с его отрицанием.
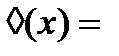
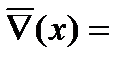
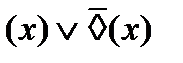– закон исключения случайности
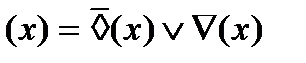
Рассматривая 2 таблицы можно определить эквивалентные преобразования операторов.
|
|
| 
| 
| 
|
| 
| 
|
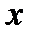
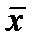
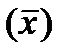
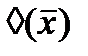
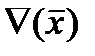
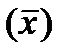
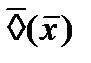
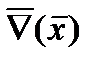
Рис. 30.
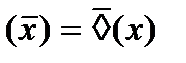
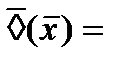
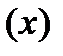
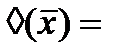
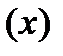
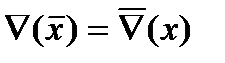
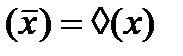
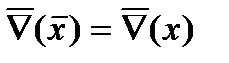
Данные преобразования модальных операторов применяются для минимизации трехзначных функций и для получения эквивалентных функций.
Модальные операторы являются расширением двузначной записи в логике Буля.
Для описания трехзначных функций Лукасевич ввел собственный вид представления.
Любая функция раскладывается следующим образом:
| терм |
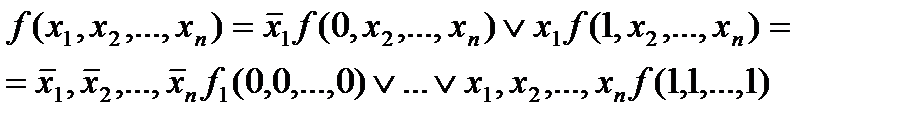
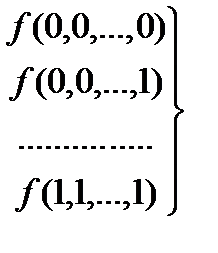множество констант
При таком разложении функции в конечном итоге каждый терм умножается на некоторую константу.
Таким образом получается, что в окончательной записи функции присутствуют только те термы, у которых значение константы равно 4.
Лукасевич предложил раскладывать функцию на 3 составляющие:
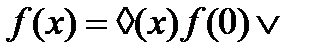
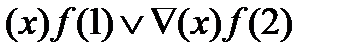
В окончательной записи функции будут присутствовать только те термы, у которых const = 1 или 2.
Рассмотрим запись трехзначной функции в виде таблицы и аналитически.
| х1 | х2 | F |
Для минимизации используются карты Лукасевича. Объединение переменных в терм выполняется по закону 3i,
| х1 х2 | |||
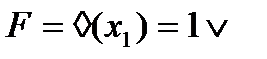
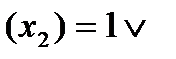
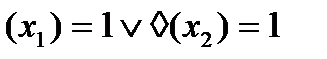
Для минимизации функции используются графические и аналитические методы. В графическом функция представляется в виде гиперкуба (склеивание по вершинам, ребрам, плоскостям).
ЛЕКЦИЯ 11,12.
