2015-07-14
605
Во всех рассуждениях данного раздела предполагается, что бинарное отношение предпочтения 
определено на Р - множестве всех простых распределений вероятностей р, q,..., заданных на непустом множестве Х. Элементами Х могут быть чистые стратегии или альтернативы, либо же они могут представлять собой исходы, или последствия, некоторых решений, принимаемых в ситуациях, содержащих элемент риска; вероятности таких исходов описываются некоторым распределением из Р.
Простым распределением вероятностей р называется вещественная функция Р, которая принимает положительные значения на большинстве элементов х из конечного множества Х, а сумма всех значений р(х) равна единице. В зависимости от контекста распределения из Р часто называют ставками, играми, лотереями, альтернативами риска, смешанными стратегиями и рандомизированными стратегиями. Для любых распределений р и q из Р выражение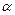 
р+(1- 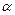)q называется прямой линейной комбинацией распределений p и q; здесь 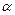- действительное число, заключенное между 0 и 1. Таким образом, если r= 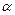р+(1- 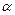)q, то
|
|
|
r(х)= 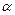р(х)+(1- 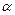)q(х) (1.3)
для любого х из Х. Если р и q принадлежат Р и 0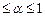 
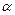, то р+(1- 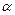)q также принадлежит Р.
Предположим, что при 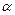=0,5 элементами Х являются некоторые суммы денег и пусть распределение P имеет вид:
р(0 долл.)=0,3;
р(10 долл.)=0,2;
р(20 долл.)=0,5,
а распределение q -
q(7 долл.)=0,7;
q(10 долл.)=0,3.
Тогда
r(x)= 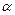р(x)+(1- 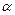)q(x)= 
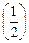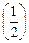p(x)+ q(x);
r(0 долл.)=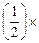 
0+ 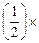0,3=0,15;
r(7 долл.)= 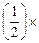0+ 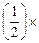0,7=0,35;
r (10 долл.)= 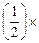0,2+ 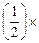0,3=0,1+0,15=0,25;
r(20 долл.)= 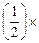0,5+ 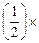0=0,25.
Проведем проверку:
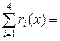0,15+0,35+0,25+0,25=1,0.
Таким образом, прямая линейная комбинация (1.3) простых распределений вероятностей P и Q привела к простому распределению вероятностей R.
