Аксиомы для линейной функции полезности

В данном разделе будут рассмотрены аксиомы (или условия) для отношения на множестве Р, выполнение которых означает, что существует линейная функция полезности для отношения на Р. Аксиом A1, А2, АЗ достаточно для существования линейной функции полезности для отношения на Р. Выполнение аксиом В1, В2, ВЗ обеспечивает необходимые и достаточные условия существования совершенной линейной функции полезности для отношения на множестве Р. В каждом случае Х представляет собой любое непустое множество, причем не обязательно конечное или исчислимое. Аксиомы не означают, что полезность ограничена, хотя ограниченность полезности обычно возникает в результате применения аналогичных аксиом к непростым распределениям вероятностей.

Первоначальная аксиоматика для совершенной функции полезности была предложена Нейманом и Моргенштерном, и поэтому совершенную линейную функцию u на P (или дополнительную к ней функцию v на Х) часто называют функцией полезности Неймана - Морген­штерна. Используется также выражение «полезность по Бернулли», поскольку Бернулли внес вклад в разработку этого вопроса.

При формулировке каждой аксиомы предполагается, что все р, q, r и s принадлежат множеству Р.

Аl. Отношение на Р не рефлексивно.

А2. Если 0< < 1, р q и r s, то р + (1- )r q+(1- ) s.

АЗ. Если р q и r s, то р+(1- )s q+(1- )r для некоторого , заключенного строго между 0 и 1.

В1. Отношение на Р является слабым упорядочением.

В2. Если 0< < 1 и р q, то р + (1- )r q+(1- ) r.

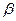ВЗ. Если р q и q r, то р+(1- )r q и q p+(1- 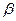)r для некоторых и 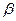, лежащих строго между 0 и 1.

Аксиомы А1 и В1 уже обсуждались выше (они означают, что отношение ациклично); аксиомы А2 и В2 называют по-разному: аксиомами независимости, аддитивности или условиями линейности. Линейные свойства функции u (1.4) получаются непосредственно из этих аксиом. Рациональное обоснование аксиом А2 и В2 обычно дается следующим образом: сначала выбирают р и r с соответствующими вероятностями а и (1- ), а затем составляют выражение р+(1- )r на основе ранее сделанного выбора. Такой подход представляется достаточно разумным, но иногда вызывает возражения с психологической точки зрения. Поясним аксиому А2 с помощью следующего примера. Запишем диаграмму и будем считать, что мы выбираем строку А или B, а нейтральный наблюдатель выбирает столбец с вероятностями и (1- ):

		1-
A	p	r
B	q	s

После выбора строки и столбца получаем соответствующие р, q, r и s. Если мы предпочитаем р по сравнению с q и r по сравнению с s, то первая строка A строго доминирует вторую строку B в смысле нашего предпочтения; но это наводит на мысль, что мы будем (или даже должны) выбирать А вместо В, не обращая никакого внимания на значение величины . Поскольку А и В характеризуются выражениями р(1- )r и q+(1- )s, то имеем: если р q и r s, то р+(1- )r q+(1- )s.

Аналогично можно обосновать аксиому В2, заменив s на r в приведенной: диаграмме, где >0. Если р q, то (так как r~r) представляется разумным предположить (или предложить), что А будет выбираться вместо В или что р + (1- ) r 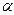q +(1- 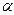)r. С психологической точки зрения определенная «слабость» аксиомы В2 заключается в некотором пренебрежении краевыми эффектами. Если очень мало (близко к нулю), то субъ­ект может на самом деле и не стараться уловить различия между А и В (или он просто не в состоянии это сделать), поэтому ему будет безразлично, что выбирать: А или В. Такой критике нельзя подвергнуть аксиому А2, поскольку в ней как р q, так и r s.

Последними в данных наборах аксиом являются аксиомы А3 и В3, которые часто называют аксиомами Архимеда или условиями непрерывности. Смысл их введения состоит в том, чтобы вместе с другими аксиомами обеспечить существование вещественных функций полезности; с этой точки зрения они играют ту же роль, что и условие «плотности относительно упорядочения» из подраздела 1.2.3.

Аксиома А3 сильнее, чем В3, поскольку она включает условие аксиомы В3. Чтобы продемонстрировать очевидную разумность этих аксиом, достаточно положить 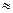1 в аксиоме А3 или взять 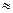1, а 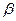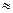0 в аксиоме В3.