Аксиоматика в области субъективной ожидаемой полезности опирается в основном на первую из описанных выше схем построения теории, на которой мы и сосредоточим наше внимание в заключение данной главы.
Самая элегантная формальная теория в рамках первой схемы разработана Сэвиджем. Теории ожидаемой полезности Сэвиджа предшествовала схема Рамсея.
Рамсей предлагал использовать «нейтральное» утверждение (нечто, равносильное событию Е с вероятностью 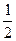 ) для измерения полезности исходов путем процедуры последовательного деления пополам. В процедуре для общности требуется бесконечность множества Х. Пусть элементами Х являются некоторые суммы денег (ранжированные от большего предпочтения к меньшему) и х>z; тогда получается элемент у в промежутке между х и z, такой, что он гарантированно находится в отношении безразличия с {х, если событие Е осуществляется, и z, если событие Е не наступает}. Затем полагаем v(y)=
) для измерения полезности исходов путем процедуры последовательного деления пополам. В процедуре для общности требуется бесконечность множества Х. Пусть элементами Х являются некоторые суммы денег (ранжированные от большего предпочтения к меньшему) и х>z; тогда получается элемент у в промежутке между х и z, такой, что он гарантированно находится в отношении безразличия с {х, если событие Е осуществляется, и z, если событие Е не наступает}. Затем полагаем v(y)= 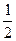 v(x)+
v(x)+ 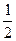 v(z). После этого функция v на X используется как мера вероятностей для p*: пусть A - событие (подмножество S) и для x, y, z имеем v(x)>v(y)>v(z), причем у гарантированно находится в отношении безразличия к {х, если событие А наступает, или z, если А не осуществляется}; тогда р*(А) определяется из равенства v(у)=Р*(А)v(х)+[1-Р*(А)]v(z). В некоторых теориях предполагается существование полного набора внешних вероятностных мер, которые позволяют при конечном множестве Х получить единственную, с точностью до аффинного преобразования, функцию v.
v(z). После этого функция v на X используется как мера вероятностей для p*: пусть A - событие (подмножество S) и для x, y, z имеем v(x)>v(y)>v(z), причем у гарантированно находится в отношении безразличия к {х, если событие А наступает, или z, если А не осуществляется}; тогда р*(А) определяется из равенства v(у)=Р*(А)v(х)+[1-Р*(А)]v(z). В некоторых теориях предполагается существование полного набора внешних вероятностных мер, которые позволяют при конечном множестве Х получить единственную, с точностью до аффинного преобразования, функцию v.
Сэвидж действует противоположным образом по сравнению с описанной процедурой «измерений». Прежде всего, он вводит вероятностную меру P* на основе своих аксиом для отношения  на Р. При этом он использует процедуру деления пополам, в которой предполагается бесконечность множества S. Пусть х предпочтительнее у и некоторый субъект считает, что в отношении безразличия находятся {х, если наступает А, или y, если не осуществляется А} и {у, если осуществляется А, или х, если А не осуществляется}; тогда из равенства P*(A)v(х)+[1-P*(А)]v(у)=Р*(А)v(у)+[1-Р*(А)]v(х) получается р*(А)=
на Р. При этом он использует процедуру деления пополам, в которой предполагается бесконечность множества S. Пусть х предпочтительнее у и некоторый субъект считает, что в отношении безразличия находятся {х, если наступает А, или y, если не осуществляется А} и {у, если осуществляется А, или х, если А не осуществляется}; тогда из равенства P*(A)v(х)+[1-P*(А)]v(у)=Р*(А)v(у)+[1-Р*(А)]v(х) получается р*(А)= 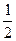 независимо от конкретных значений v(х) и v(у) [до тех пор, пока v(х)
независимо от конкретных значений v(х) и v(у) [до тех пор, пока v(х) 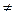 v(у)]. Рассмотрим диаграмму
v(у)]. Рассмотрим диаграмму
| B | A-B | A | |
| Выбор 1 | x | y | x |
| Выбор 2 | y | x | x |
Здесь В является «подсобытием» события А и А-В означает событие: «А произошло, а В - нет». Если х не находится в отношении безразличия к у, но (выбор 1)~(выбор 2), то из модели субъективной ожидаемой полезности с помощью непосредственных выкладок получаем P*(В)= 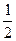 P*(А).
P*(А).
После того как будет получена мера Р*, с ее помощью можно получить функцию v на Х. Пусть х предпочтительнее у, который в свою очередь предпочтительнее z, и пусть А является событием, которое состоит в том, что у приводится в отношение безразличия к {х, если осуществляется А, или z, если А не осуществляется}; тогда v(х), v(у), v(z) связаны друг с другом посредством равенства v(у)=P*(А)v(х)+[1-р*(А)]v(z). Фактически, как отмечал еще Сэвидж, его аксиомы означают, что P* приводит к множеству индуцированных мер pf на Х для различных f из А, обладающих структурой, которую Нейман и Моргенштерн использовали в своей теории ожидаемой полезности (подраздел 1.3.2). Следовательно, при заданной P* существование подходящей функции v на Х следует из ранее развитой теории.
Мы не будем рассматривать различные структурные условия, но коротко остановимся на одной новой аксиоме, которая, по существу, не фигурировала в теоретических построениях в подразделе 1.3. Эта аксиома имеет вид условия независимости и регулярности для событий и исходов. Подход Рамсея гарантирует, что, если v(х)>v(у)>v(z), v(х')>v(у')>v(z'); если 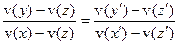 и у находится в отношении безразличия к {х, если осуществляется А, или z, если А не осуществляется}, то у' безразличен к {х', если осуществляется А, или z', если не осуществляется А}. В результате P*(А) однозначно определяется через отношение разностей функции v. С точки зрения Сэвиджа, гарантировано, что если р*(А)=р*(B), х предпочтительнее, чем у, а у предпочтительнее, чем z, и если у находится в отношении безразличия к {х, если осуществляется А, или z, если не осуществляется А}, то у безразличен к {х, если осуществляется В, или z, если В не осуществляется}. Тогда величина P*(А) однозначно определяется как отношение
и у находится в отношении безразличия к {х, если осуществляется А, или z, если А не осуществляется}, то у' безразличен к {х', если осуществляется А, или z', если не осуществляется А}. В результате P*(А) однозначно определяется через отношение разностей функции v. С точки зрения Сэвиджа, гарантировано, что если р*(А)=р*(B), х предпочтительнее, чем у, а у предпочтительнее, чем z, и если у находится в отношении безразличия к {х, если осуществляется А, или z, если не осуществляется А}, то у безразличен к {х, если осуществляется В, или z, если В не осуществляется}. Тогда величина P*(А) однозначно определяется как отношение 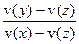 .
.
 2015-07-14
2015-07-14 1106
1106








