Лекция 3. Производная функции одной переменной
1. Задачи, приводящие к понятию производной.
2. Определение производной функции одной переменной.
3. Основные формулы дифференцирования.
Задача о скорости движения
Пусть вдоль некоторой прямой движется точка по закону 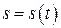 , где
, где 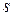 - пройденный путь,
- пройденный путь, 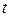 - время, и необходимо найти скорость точки в момент
- время, и необходимо найти скорость точки в момент 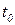 .
.
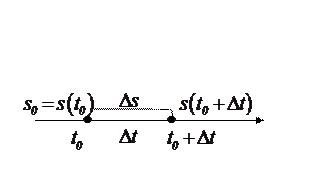 | К моменту времени 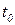 пройденный путь равен пройденный путь равен 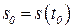 , а к моменту , а к моменту 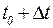 - путь - путь 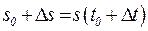 (см. рис.). Тогда за промежуток (см. рис.). Тогда за промежуток 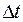 средняя скорость будет средняя скорость будет 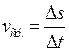 . Чем меньше . Чем меньше |
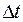 , тем лучше средняя скорость характеризует движение точки в момент
, тем лучше средняя скорость характеризует движение точки в момент 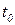 . Поэтому под скоростью точки в момент
. Поэтому под скоростью точки в момент 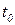 естественно понимать предел средней скорости за промежуток от
естественно понимать предел средней скорости за промежуток от 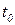 до
до 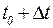 , когда
, когда 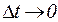 , т.е.
, т.е.
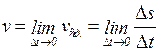 (1.1)
(1.1)
 2015-07-14
2015-07-14 1021
1021