Теорема. Если функция 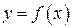 дифференцируема в точке
дифференцируема в точке 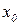 , то она непрерывна в этой точке (обратное не верно).
, то она непрерывна в этой точке (обратное не верно).
Теорема. Если 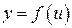 и
и 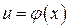 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции 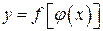 существует и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной:
существует и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной:
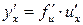
Таблица производных
Основные правила дифференцирования
1. 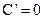
2. 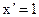
3. 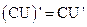
4. 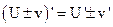
5. 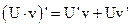
6. 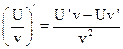
Основные формулы дифференцирования
Здесь 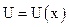 | Здесь х - аргумент | Здесь 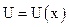 | Здесь х - аргумент |
1. 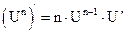 2. 2. 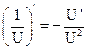 3. 3. 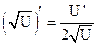 4. 4. 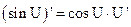 5. 5. 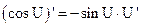 6. 6. 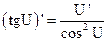 7. 7. 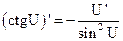 8. 8. 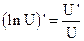 | 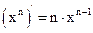 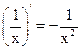 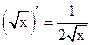 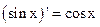 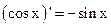 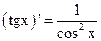 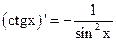 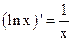 | 9. 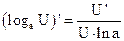 10. 10. 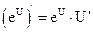 11. 11. 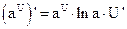 12. 12. 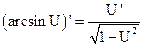 13. 13. 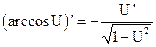 14. 14. 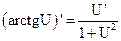 15. 15. 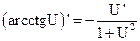 | 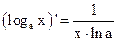 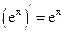 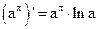 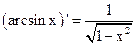 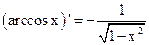 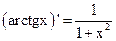 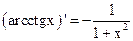 |
Задача. Найти производные функций
1. 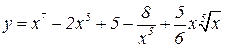
2. 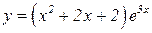
3. 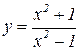
4. 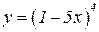
5. 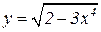
6. 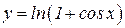
7. 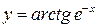
8. 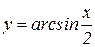
9. 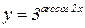
10. 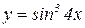
 2015-07-14
2015-07-14 758
758







