2015-07-14
498
Пусть функция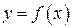 
определена на промежутке 
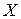. Возьмем точку 
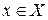. Дадим значению х приращение 
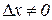. Тогда функция получит приращение 
.
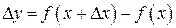Определение. Производной функции 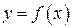называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
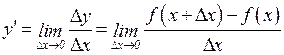(2.1)
Производная функции имеет несколько обозначений: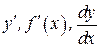 
. Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например 
.
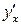Нахождение производной функции называется дифференцирование м этой функции.
Из задачи о скорости движения следует механический смысл производной: производная пути по времени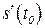 
есть скорость точки в момент 
: 
.
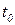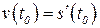Из задачи о производительности труда следует экономический смысл производной: производная объёма произведённой продукции по времени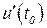 
есть производительность труда в момент .
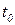Геометрический смысл производной: производная функции 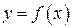в точке 
(
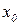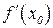) есть угловой коэффициент (тангенс угла наклона) касательной, проведённой к кривой 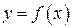в точке 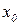, т.е. 
.
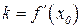Уравнение касательной к кривой 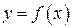в точке 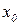имеет вид
