Автоматы и преобразователи с магазинной памятью

Принцип работы: Автоматы и преобразователи с магазинной памятью – это машины Тьюринга с входной лентой, в которых работа с рабочей лентой определяется следующим образом: управляющая головка всегда указывает на крайний правый непустой символ ленты и за один такт возможны следующие действия:

а) стирание крайнего правого символа (запись пустого символа) и сдвиг головки на одну ячейку влево;

б) стирание крайнего правого символа и запись на рабочую ленту непустой цепочки.

Простейшим классом машин Тьюринга являются конечные автоматы – это машины Тьюринга с входной (в случае конечного преобразователя – и с выходной) лентой, но без рабочей ленты.

F Определение: Конечным автоматом называется упорядоченная пятерка следующих объектов:

А =(K, S, d, q ₀, F),

где К – конечное множество состояний машины;

S – конечное множество входных символов;

d: К ´ S Þ К;

q ₀ – начальное состояние;

F – подмножество множества К (заключительных состояний).

Если функция δ — однозначная, то А называют детерминированным. Если функция δ — многозначная, то А называют недетерминированным.

Конфигурация автомата (q, w) Î К ´ S*, при этом начальная конфигурация (q₀, w) и конечная конфигурация (q,ε) \ q Î F. Здесь w — цепочка символов, которые еще не были обработаны.

Напомним, что переходы от конфигурации к конфигурации за один такт обозначаются знаком |¾, за несколько тактов знаком |¾^*. Распознаватель А = (K, S, d, q ₀, F) допускает входную цепочку w Î S*, если (q₀,w) |¾^* (q,ε), q Î F.

Язык, определяемый конечным автоматом А,

L(А) = {w Î S*\ (q₀,w) |¾^* (q,ε), q Î F}

Язык L(А) назовем регулярным, если для него можно построить распознающий конечный автомат.

Пример 13: Конечный автомат, допускающий цепочки из 0 и 1, в которых имеется подцепочка 11.

А = ({q₀, q₁, q₂}, { 0, 1}, δ, q_0, {q₂}) Функция переходов:

δ(q ₀, 0) = {q ₀ }, δ(q ₀, 1) = {q ₁ }, δ(q ₁ ,0) = {q ₀ }, δ(q₁,1) = {q₂}, δ(q₂,0) = {q₂}, δ(q₂,1) = {q₂}

Конечный автомат удобно задавать диаграммой его переходов. Диаграмма представляет собой ориентированный граф, вершины которого одноименны состояниям автомата; дуга из вершины q _i, в вершину q_k с надписанной над ней буквой а_j проводится тогда и только тогда, когда δ (q_i,а_j)=q_k. В случае, когда переход из q_i в q_k осуществляется под воздействием любой из букв некоторого подмножества S, SÍS, все буквы этого подмножества подписываются над соответствующей дугой (вместо перечня всех букв допускается сокращенная запись «xÎS» или просто «S»). Если произвольное состояние q_i входит в F, то данный факт на диаграмме отмечается жирным кружком, выделяющим вершину q_i.

Очевидно, что любой конечный автомат полностью определяется своей диаграммой переходов. Далее под задачей построения конечного автомата, обладающего теми или иными свойствами, будет пониматься задача построения диаграммы его переходов.

Пример 14:

На рис. 2 показана диаграмма автомата А₁, работающего над словами алфавита S ={a,b,c}. Автомат имеет два состояния, q₀ и q₁, причем «хорошим» является только состояние q₁. Начав работу в состоянии q₀, автомат под воздействием букв a, b из этого состояния не выходит; под воздействием буквы с реализуется переход в состояние q₁; любая далее поступающая буква оставляет автомат в том же состоянии. Таким образом, автомат А₁, распознает язык L₁, состоящий из слов, имеющих в своем составе букву с. Данный язык является регулярным.

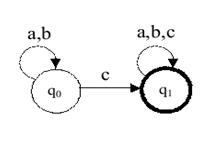
Рис.2.

Пример 15:

На рис. 3 показана диаграмма автомата А₂, работающего над словами алфавита S ={a,b,c}. Автомат А₂, распознает язык L₂ - множество слов, в которых буква а встречается четное число раз.

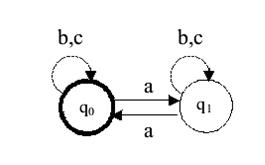
Рис. 3.

Пример 16:

На рис. 4 показана диаграмма автомата А₃, работающего над словами алфавита S ={a,b,c}. Автомат А₃, распознает язык L₃ - множество слов, начинающихся и заканчивающихся одинаковой буквой.

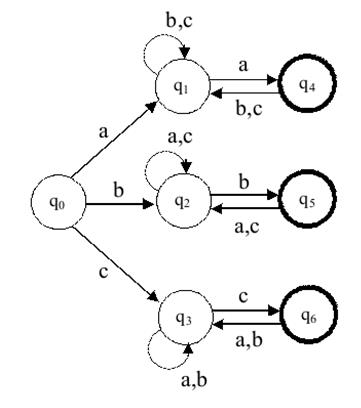
Рис.4

Множество языков, допускаемых конечными автоматами, совпадает с множеством языков, порождаемых автоматными грамматика­ми.

F Определение: Автоматом с магазинной памятью (МП-автоматом) называется следующая семерка объектов:
М =(K, Н, S, d, Z ₀, q ₀, F),

где К – конечное множество состояний машины;

Н – конечное множество символов магазинной памяти (стека);

S – конечное множество входных символов;

d: К ´S´ Н Þ К ´ Н *;

Z ₀Î H – выделенный элемент из Н (граничный маркер);

q ₀ – начальное состояние;

F – подмножество заключительных состояний.

Лемма 6: По любой УКС грамматике можно построить упрощенный недетерминированный МП-автомат, допускающий язык, порождаемый этой грамматикой.

На каждом такте работы МП-преобразователь, кроме обычных действий автомата, может записать на выходную ленту некоторую цепочку символов из специального множества выходных символов.

Конфигурация МП-автомата: q — состояние устройства управления, x — необра­ботанная часть входной цепочки я α — содержимое магазина.

Начальная конфигурация (q₀, w, Z₀) заключительная конфигурация (q,ε,α).

Такт работы (q,x,α) |¾ (q',x',α').

МП-автомат допускает цепочку символов w Î S *, если (q₀, w, Z₀) |¾^* (q,ε,α) при некоторых q Î F и α Î H *.

Язык, определяемый (допускаемый) МП-автоматом, образуют все распознавае­мые им цепочки.

Пример 17:

Рассмотрим язык чисел, порождающая грамматика которого имеется в разделе 3.3. Для этого языка построим детерминированный МП-автомат имеющий 2 состояния: q₀ и q₁ из которых q₀ — начальное, a q₁ —заключительное, и 5 символов магазинной памяти: Z₀. А, В. С, D. Содержательно символ Z₀ будем играть роль граничного маркера, А — означать, что анализируется целая часть десятичного числа (возможно, пустая); В — использоваться при анализе дробной части десятичного числа, D — порядка. С — символ, используемый при анализе возможного знака порядка. В магазинной памяти всегда будет записан лишь один из этих символов. Так как число заканчивается цифрой, автомат после чтения цифры всегда будет находиться в состоянии q₁, а после чтения любого другого символа, который может использоваться в числах,— в состоянии q₀. Приведем таблицу функции d, которая после сделанных замечаний не требует особых пояснений.

1. d (q _o ,+, Z₀) = (q _o , A); 11. d (q _o, -, C) = (q _o, D);

2. d(q _o , -, Z₀) = (q _o , A); 12. d (q _o, d, C) = (q ₁, D);

3. d (q _o,., Z_o) = (q _o , B): 13. d(q _o ,d, D)=(q ₁, D);

4. d(q _o ,e, Z_o)=(q _o, C); 14. d(q ₁,., A) = (q _o, B);

5. d(q _o, d, Zo) = (q ₁, A); 15. d (q ₁ ,e, A) = (q _o, C);

6. d(q _o,., A)= (q _o, B); 16. d (q ₁, d, A) = (q ₁ , A);

7. d(q _o ,e, A) = (q _o , С); 17. d (q ₁ ,e, В) = (q _o , С);

8. d (q _o, d, A) = (q ₁, A); 18. d (q ₁, d, B) = (q ₁, B);

9. d(q _o, d, B)=(q ₁, B); 19.d(q₁,d,D)=(q₁,D).
10. d(q _o, +, C)=(q _o, D);

Здесь d означает любую цифру, и соответствующие строки таблицы определяют, таким образом, по 10 значений функции. Как и в большинстве других случаев, в данном примере функция d является частично определенной. Будем считать, что если в процессе работы автомата встретилась комбинация состояния и символов, для которой значение d не определено, автомат прекраща­ет работу, а анализируемая цепочка не входит в язык, распозна­ваемый автоматом. Такое допущение не является принципиальным, так как частично определенную функцию d можно всегда тривиальным образом доопределить не меняя язык, определяемый автоматом.

Рассмотрим анализ с помощью описанного автомата цепочек основных символов языка чисел, выписывая соответствующие последовательности конфигураций автомата. Число +13.2e-4 анализируется следующим образом:

(q₀, + 13.2 e-4, Z₀), (q₀, 13;2 e- 4, A), (q₁ , 3.2e-4, А), (q₁ ,. 2e-4, А), (q₀, 2e-4, В), (q₁ e-4, В), (q_0t -4, С), (q₀, 4, D), (q_0, e,D).

Так как автомат находится в заключительном состоянии, ана­лиз прошел успешно, и входная цепочка принадлежит языку.

Отметим, что, множество чисел построенного языка является регулярным. Поэтому существует распознающий это множество конечный автомат. Этот автомат может быть получен из приведенного МП-автомата, для чего нужно поставить в соответствие каждой возможной комбинации состояния и символа магазинной памяти МП-автомата состояние конечного автомата и преобразовать соответствующим образом таблицу функций. Так как в магазинной памяти МП-автомата всегда содержится только один символ, полученный конечный автомат будет распознавать тот же язык

На каждом такте работы МП-преобразователь, кроме обычных действий автомата, может записать на выходную ленту некоторую цепочку символов из специального множества выходных символов.

F Определение: Преобразователи с магазинной памятью (МП – преобразователем) называется следующая восьмерка объектов: S =(K, S, H, D, m, Z ₀, q ₀, F), где

К – конечное множество состояний машины;

Н – конечное множество символов магазинной памяти (стека);

S – конечное множество входных символов;

D - конечное множество символов выходной ленты;

m: K ´S´ H Þ K ´ H *´D*;

Z ₀Î H – выделенный элемент из Н (граничный маркер);

Q ₀ – начальное состояние;

F – подмножество заключительных состояний.

Свойства МП – преобразователей аналогичны свойствам МП-автоматов.