1. Определение двойственной задачи к задаче ЛП в каноническом виде;
2. Определение двойственной задачи к задаче ЛП в нормальном виде;
3. Шесть соотношений двойственности.
ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Лабораторная работа 5
Метод удобно применять к задачам линейного программирования, для которых известен или легко строится начальный двойственный базисный план (или соответствующий ему коплан), а также, к уже решенным симплекс-методом задачам в случае изменения вектора условий 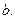
Алгоритм. Пусть дана задача линейного программирования
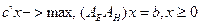 (1)
(1)
(обозначения те же, что и в лабораторной работе 2, 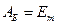 ).
).
Двойственная к (I) задача (см. лабораторную работу 4) имеет вид
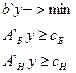 (2)
(2)
Предположим теперь, что 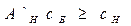 , тогда вектор
, тогда вектор 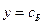 начальный двойственный базисный план задачи (1).
начальный двойственный базисный план задачи (1).
Ему соответствует базисный коплан 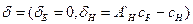 и базисный псевдоплан æ=(æБ
и базисный псевдоплан æ=(æБ 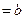 ,æ н= 0)
,æ н= 0) 
1. Строим начальную двойственную симплекс-таблицу.
2. Проверяем выполнение критерия оптимальности. Если ӕБ ≥ 0, то вектора y, ӕ –оптимальные планы задач (2), (1), а если 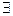 æ j < 0,
æ j < 0, 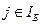 , то идем к пункту 3.
, то идем к пункту 3.
3. Проверяем достаточное условие отсутствия прямых планов. Если
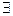 æ j < 0,
æ j < 0, 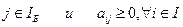 (3)
(3)
то ограничения задачи (1) несовместимы. Если условие (3) не имеет места, то переходим к пункту 4.
4. Совершаем двойственную симплекс-итерацию – переход к новому базисному коплану:
а) Строим новый базис с индексным множеством 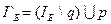 , где p и q находятся из соотношений
, где p и q находятся из соотношений
 æ q =
æ q = 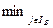 æ j,
æ j, 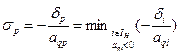
Элемент таблицы 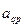 - разрешающий.
- разрешающий.
б) Строим новую двойственную симплекс-таблицу, совершая основное симплексное преобразование по элементу 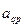 :
:
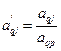 , æ
, æ 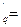 æ
æ 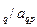
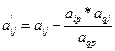 , æ
, æ 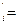 æ i − æq*
æ i − æq* 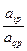
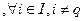
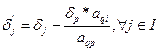
5. К новой таблице применяем п.2 алгоритма и т.д.
Замечание. Расчет новой таблицы нужно начинать с определения значений столбца 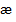 и строки
и строки 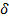 , так как если выполняется критерий оптимальности (см.п.2), то нет необходимости вычислять оставшуюся часть таблицы.
, так как если выполняется критерий оптимальности (см.п.2), то нет необходимости вычислять оставшуюся часть таблицы.
Пример. Решить двойственным симплекс-методом задачу
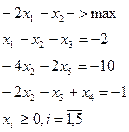 (3)
(3)
Решение:
1. Приводим задачу (3) к виду (1)
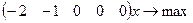
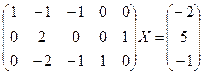
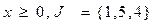 (4)
(4)
2. Строим двойственную задачу к задаче (4).
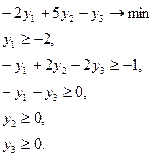
Вектор 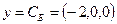 является невырожденным двойственным базисным, так как
является невырожденным двойственным базисным, так как 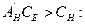
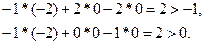
3. Вычисляем базисный коплан и базисный псевдоплан, составляем начальную двойственную симплекс-таблицу и применяем двойственный симплекс-метод.
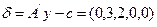
æ =(-2,0,0,-1,5)
 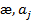 Базис
Базис
| 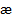
| 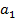
| 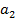
| 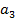
| 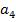
| 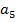
| Табл.1 Табл.2 |
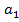
| -2 | -1 |  -1 -1
|  0 0
| |||
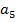
| |||||||
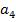
| -1 | -2 | -1 | - | |||
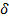
| |||||||
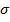
| 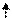 2 2
| ||||||
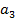
| -1 | ||||||
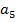
| |||||||
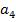
| -1 | -1 | |||||
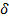
| -1 | ||||||
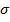
|
4. Таблица 2 задает оптимальный план задачи (3):
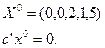
Задание. Двойственным симплекс-методом решить следующие задачи:
1.
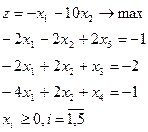
| 2.
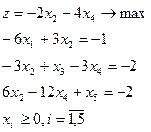
|
3.
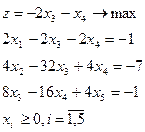
| 4.
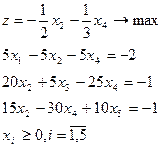
|
5.
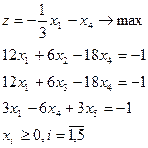
| 6.
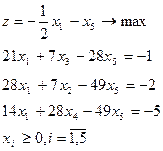
|
7.
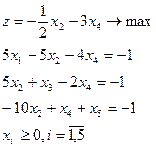
| 8.
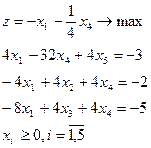
|
9.
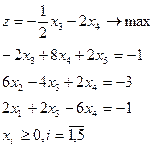
| 10.
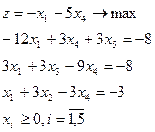
|
11.
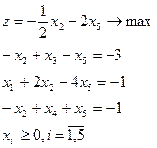
| 12.
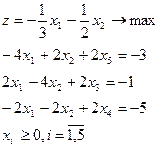
|
13.
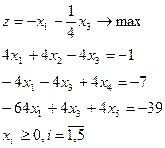
| 14.
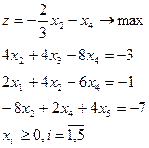
|
15.
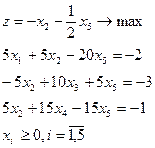
| 16.
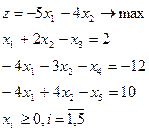
|
17.
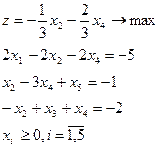
| 18.
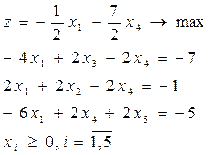
|
19.
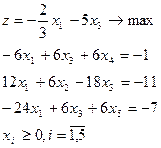
| 20.
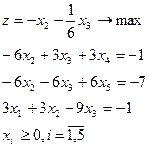
|
21.
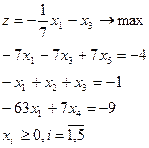
| 22.
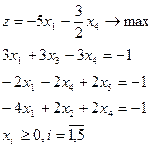
|
23.
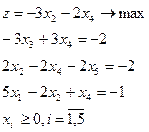
| 24.
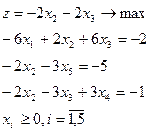
|
25.
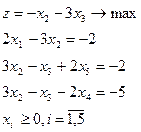
| 26.
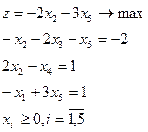
|
 2015-07-14
2015-07-14 369
369








