1. Постановка задачи линейного программирования в канонической форме,
2. Определение базисного плана;
3. Критерий оптимальности в симплекс-методе;
4. Достаточное условие неограниченного возрастания целевой функции;
5. Алгоритм симплекс-метода, правило прямоугольника.
ДВУХФАЗНЫЙ СИМПЛЕКС МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Лабораторная работа 3
Дана задача линейного программирования в канонической форме:
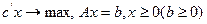 | (1) |
Предположим, что она не обладает свойствами, при которых применим симплекс-метод (см. лаб. раб. 2). В этом случае задачу (1) следует решать двухфазным симплекс-методом.
Алгоритм. Первая фаза. Построение начального базисного плана задачи (1).
1) Составляем задачу первой фазы
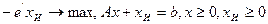 | (2) |
Где 
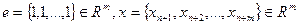 - вектор искусственных переменных.
- вектор искусственных переменных.
2) Задачу (2) решаем симплекс-методом. Для неё 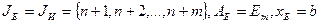 .
.
3) Пусть решение задачи (2) - 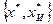 задается таблицей
задается таблицей 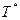 с множеством базисных индексов
с множеством базисных индексов 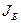 и элементами
и элементами 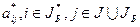 .
.
Возможны три случая:
а) Если 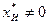 , то исходная задача не имеет планов. Процесс решения окончен.
, то исходная задача не имеет планов. Процесс решения окончен.
б) Если 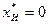 и
и 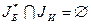 (среди базисных планов нет искусственных), то
(среди базисных планов нет искусственных), то  - базисный план задачи (1) с базисным множеством
- базисный план задачи (1) с базисным множеством 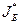 .
.
в) Если 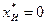 , но
, но 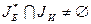 (среди базисных переменных имеются искусственные), то для
(среди базисных переменных имеются искусственные), то для 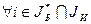 возможны два подслучая:
возможны два подслучая:
в1) Если в строке, соответствующей переменной 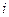 таблицы
таблицы 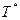 имеется элемент
имеется элемент 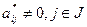 , то, выбирая
, то, выбирая 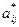 за разрешающий элемент и выполняя с ним симплексное преобразование, исключаем искусственную переменную
за разрешающий элемент и выполняя с ним симплексное преобразование, исключаем искусственную переменную 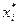 из базисных, а
из базисных, а 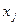 вводим в состав базисных переменных;
вводим в состав базисных переменных;
в2) Если же в этой строке все 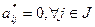 , то в системе ограничений задачи (2)
, то в системе ограничений задачи (2) 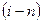 уравнение есть следствие остальных уравнений. Его нужно из (2) удалить, а из
уравнение есть следствие остальных уравнений. Его нужно из (2) удалить, а из 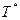 - таблицы вычеркнуть указанную i -ю строку и j -й столбец.
- таблицы вычеркнуть указанную i -ю строку и j -й столбец.
Выполнение процедур в1) и в2) над всеми элементами множества 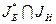 приведут к 2.б).
приведут к 2.б).
Вторая фаза. Построение оптимального плана исходной задачи (1) - (2) - (3). Принимая 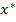 за начальный базисный план, а
за начальный базисный план, а 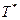 без столбцов
без столбцов 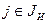 за начальную симплексную таблицу, решаем задачу (1) – (2) – (3) симплекс-методом.
за начальную симплексную таблицу, решаем задачу (1) – (2) – (3) симплекс-методом.
Замечание. В конкретных случаях при составлении задачи первой фазы (2) искусственные переменные следует вводить только в те ограничения задачи (1), в которых нет базисных переменных. Более того, в основных ограничения задачи (1) предварительно с помощью элементарных эквивалентных преобразований (умножение ограничений на положительное число, сложение ограничений) могут быть построены некоторые легко выделяющиеся базисные переменные. Все это ускоряет решение задачи первой фазы.
Пример. Двухфазным симплекс-методом решить задачу
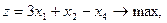 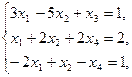 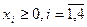 | (3) |
Решение: первая фаза.
Составляем задачу первой фазы. Так как в первой равенстве уже есть базисная переменная 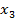 , то достаточно ввести всего лишь две искусственные переменные
, то достаточно ввести всего лишь две искусственные переменные 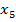 и
и 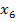 во второе и третье равенства.
во второе и третье равенства.
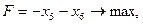 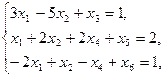 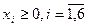 | (4) |
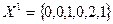 - начальный базисный план задачи (4),
- начальный базисный план задачи (4), 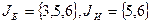 .
.
Задачу (4) решаем симплекс-методом:
с 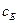 | -1 | -1 | |||||||
| Базис | b | 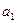 | 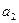 | 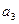 | 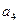 | 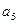 | 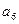 | 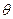 | |
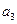 | -5 | ||||||||
| -1 | 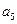 | ||||||||
| -1 | 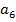 | -2 | 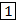 | -1 |  | ||||
| F | -3 | 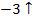 | -1 | ||||||
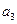 | -7 | -5 | |||||||
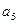 | 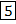 | -2 | 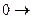 | ||||||
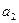 | -2 | -1 | |||||||
| F | 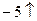 | -4 | |||||||
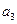 |  |  | 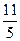 | ||||||
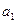 | 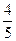 | 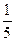 | 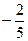 | ||||||
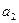 | 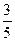 | 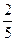 | 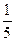 | ||||||
| F |
Последняя таблица задаёт оптимальный план задачи (4) 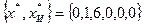 . Искусственные переменные
. Искусственные переменные  не входят в базис. Следовательно
не входят в базис. Следовательно 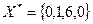 – начальный базисный план задачи (3).
– начальный базисный план задачи (3). 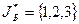 .
.
Вторая фаза. Используя последнюю таблицу, отбросив в ней столбцы 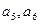 и заменив вектор стоимости с, решаем задачу (3) симплексным методом:
и заменив вектор стоимости с, решаем задачу (3) симплексным методом:
с 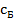 | -1 | ||||||
| Базис | b | 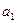 | 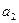 | 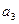 | 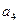 | 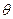 | |
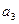 |  | ||||||
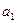 | 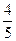 | ||||||
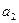 | 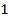 | 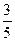 | |||||
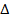 |
Так как все оценки в этой таблице неотрицательны, то она задает оптимальный план исходной задачи (3).
Ответ: Вектор 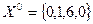 – решение задачи (3);
– решение задачи (3); 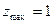 .
.
Задание. Двухфазным симплекс-методом решить следующие задачи:
1. 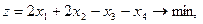 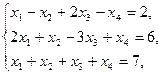 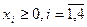 | 2. 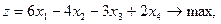 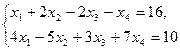  |
3. 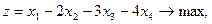 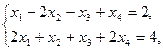  | 4. 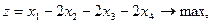 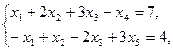 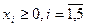 |
5. 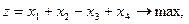 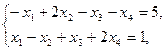  | 6. 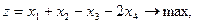 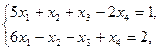  |
7. 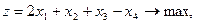 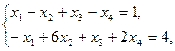  | 8. 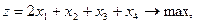 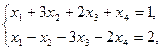  |
9. 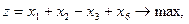 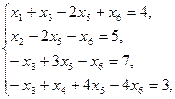 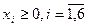 | 10. 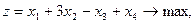 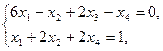  |
11. 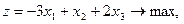 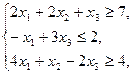 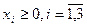 | 12. 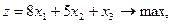 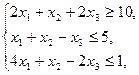 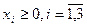 |
13. 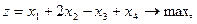 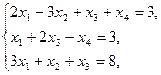 | 14. 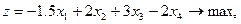 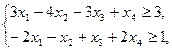  |
15. 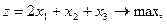 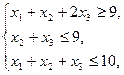 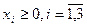 | 16. 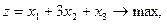 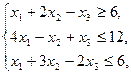 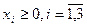 |
17. 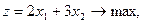 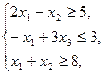 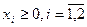 | 18. 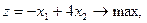  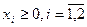 |
19. 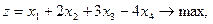 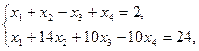  | 20. 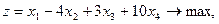 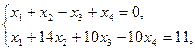  |
21. 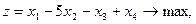 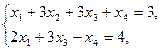  | 22. 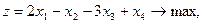 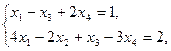  |
23. 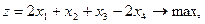 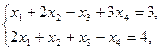  | 24. 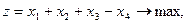 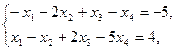  |
25. 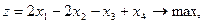 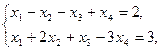  | 26. 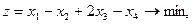 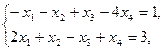  |
 2015-07-14
2015-07-14 1000
1000








