1. Математическая модель данной транспортной задачи имеет вид
Найти план перевозок
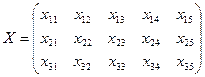
при условиях 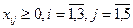 и ограничениях
и ограничениях
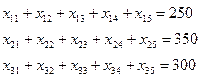
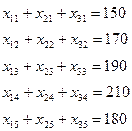
так, чтобы стоимость перевозок была минимальной:
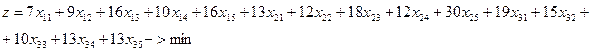
2. Проверяем выполнение условия общего баланса:
250+350+300=900, 150+170+190+210+180=900.
Задача имеет решение.
3. Строим начальный базисный план по методу минимального элемента. Решаем  задачу методом потенциалов.
задачу методом потенциалов.


| ||||||
    9 9
| -2 | -1 |   16 16
| |||
| -3 |   12 12
 70 70
| -1 |  12 12
|   30 30
| ||
| -16 | -10 |  10 10
| -8 |  13 13
| ||
| -10 | -8 | -3 | -8 |
Заметим, что 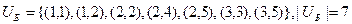 . Так как
. Так как 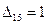 >0, то начальный план перевозок не является оптимальным. Для клетки (1,5) строим цикл. Выбираем
>0, то начальный план перевозок не является оптимальным. Для клетки (1,5) строим цикл. Выбираем 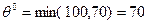 и переходим к новому базисному плану.
и переходим к новому базисному плану.
  7 7
| -3 |  10
-1 10
-1
| |||
| -3 |  12 12
|  18
-2 18
-2
| -1 | ||
| -15 |  15
-9 15
-9
| -7 |  13 13
| ||
| -9 | -7 | -3 | -7 |
Так как все оценки 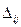 ≤0, то план перевозок оптимальный.
≤0, то план перевозок оптимальный.
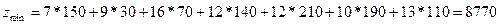
Ответ:
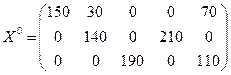 ,
, 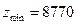 .
.
Задание. Написать математическую модель и решить транспортную задачу методом потенциалов.
| 1. | 2. | ||||||||
 

|  

| ||||||||
| 3. | 4. | ||||||||
 

|  

| ||||||||
| 5. | 6. | ||||||||
 

|  

| ||||||||
| 7. | 8. | ||||||||
 

|  

| ||||||||
| 9. | 10. | ||||||||
 

|  

| ||||||||
| 11. | 12. | ||||||||||

|  

| ||||||||||
| 13. | 14. | ||||||||||
 

|  

| ||||||||||
| 15. | 16. | ||||||||||
 

|  

| ||||||||||
| 17. | 18. | ||||||||||
 

|  

| ||||||||||
| 19. | 20. | ||||||||||
 

|  

| ||||||||||
| 21. | 22. | ||||||||||
 

|  

| ||||||||||
| 23. | 24. | ||||||||||
 

|  

| ||||||||||
| 25. | 26. | ||||||||||
 

|  

| ||||||||||
Вопросы к лабораторной работе 6:
1. Постановка транспортной задачи;
2. Математическая модель транспортной задачи;
3. Условие общего баланса;
4. Метод минимального элемента;
5. Метод потенциалов.
ОГЛАВЛЕНИЕ
1. Графический метод решения задач линейного программирования.
Лабораторная работа 1
2. Симплекс- метод решения задач линейного программирования.
Лабораторная работа 2
 2015-07-14
2015-07-14 331
331








