1. Постановка задачи первой фазы, для чего нужна первая фаза;
2. Три случая, которые возможны в результате решения задачи на первой фазе;
3. Лемма о непустоте множества планов задачи 1 фазы.
ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
Лабораторная работа 4
Все множество задач линейного программирования можно разбить на пары взаимодвойственных задач.
Для канонической формы:
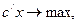
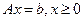 ;
;
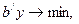
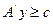 ;
;
Для нормальной формы:
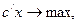
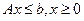 ;
;
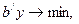
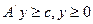 .
.
Для общей формы:
z = 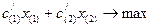 (1)
(1)
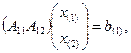
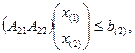
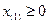
T = 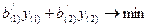
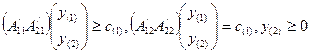 (2)
(2)
где x, c 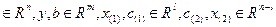 ,
,
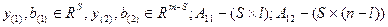 ,
,
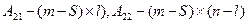 - матрицы
- матрицы
Связь между любой парой взаимодействующих задач раскрывается соотношениями двойственности.
1. Теорема существования. Для существования задачи линейного программирования необходимо и достаточно, чтобы не были пусты множества её прямых и двойственных планов.
2. Теорема двойственности. Для существования решения прямой задачи линейного программирования (1) необходимо и достаточно существования решения 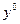 двойственной ей задачи (2). На решениях
двойственной ей задачи (2). На решениях 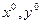 значения целевой функций задач (1), (2) равны
значения целевой функций задач (1), (2) равны
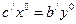 (3)
(3)
3. На каждой паре из прямого x и двойственного y планов выполняется неравенство
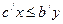 (4)
(4)
4. Достаточное условие несовместности ограничений. Если вдоль некоторой последовательности 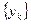
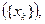 k=1,2… двойственных (прямых) планов двойственная (прямая) целевая функция неограниченно убывает (возрастает)
k=1,2… двойственных (прямых) планов двойственная (прямая) целевая функция неограниченно убывает (возрастает)
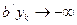 (
(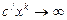 ),
), 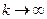 , (5)
, (5)
то задача (1) (задача (2)) не имеет планов.
5. Достаточное условие оптимальности. Если на некоторых прямом 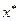 и двойственном
и двойственном 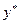 планах выполняется равенство
планах выполняется равенство
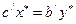 (6)
(6)
то 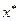 ,
, 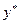 - решение задач (1) и (2).
- решение задач (1) и (2).
6. Условия дополняющей нежесткости. Планы 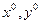 задач (1), (2) тогда и только тогда оптимальны, когда
задач (1), (2) тогда и только тогда оптимальны, когда
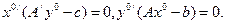 (7)
(7)
Из равенств (7) и ограничений задач (1), (2) следует:
а) если 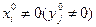 , то i-е ограничение задачи (2) (j-е ограничение задачи (1)) активно на плане
, то i-е ограничение задачи (2) (j-е ограничение задачи (1)) активно на плане 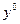 (на плане
(на плане  );
);
б) если j-е ограничение прямой задачи (i-е ограничение двойственной задачи) пассивно на плане  (на плане
(на плане 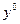 ), то
), то 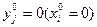 ,
, 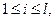
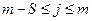 .
.
Соотношения двойственности позволяют:
1. Установить разрешимость задач.
2. Проверить оптимальность плана этой задачи по свойствам решения двойственной.
3. По оптимальному плану одной задачи найти оптимальный план двойственной.
Пример. Проверить является ли оптимальным план 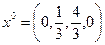 для задачи
для задачи
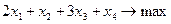
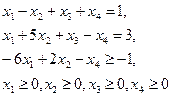 (8)
(8)
Решение.
1. Проверим, является ли  планом задачи (8). Имеем
планом задачи (8). Имеем
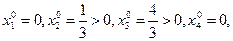 (9)
(9)
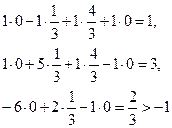 (10)
(10)
2. Приводим задачу (8) к виду (1)
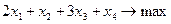
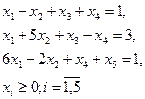 (11)
(11)
3. Строим задачу двойственную к (11).
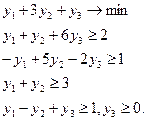 (12)
(12)
4. Предположим, что  оптимальный план задачи (11), тогда из соотношения 1 следует, что у задачи (12) есть планы, более ого существует
оптимальный план задачи (11), тогда из соотношения 1 следует, что у задачи (12) есть планы, более ого существует 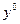 - оптимальный план для (12) (соотношение 2). По соотношению 6
- оптимальный план для (12) (соотношение 2). По соотношению 6
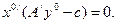
Откуда (см. п. «а») соотношения 6 и из (9) следует, что
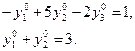
Так как на  третье ограничение задачи (11) пассивно (см.10)), то (см. п. «б» соотношения 6)
третье ограничение задачи (11) пассивно (см.10)), то (см. п. «б» соотношения 6) 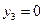 .
.
Из системы 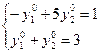 находим
находим 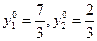 .
.
5. Проверяем является ли вектор 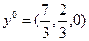 планом задачи (12)
планом задачи (12)
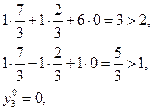
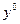 - план задачи (12).
- план задачи (12).
6. Вычисляем на  и
и 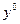 значение целевых функций задач (8) и (12)
значение целевых функций задач (8) и (12)
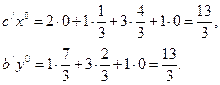
Так как 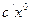 =
= 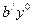 и
и  ,
, 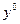 планы своих задач, то по соотношению (5) они будут решениями задач (8), (12).
планы своих задач, то по соотношению (5) они будут решениями задач (8), (12).
Задание 1. Определить, является ли вектор  решением соответствующей задачи.
решением соответствующей задачи.
Задание 2. Используя теорию двойственности, доказать оптимальность задачи минимизации (или максимизации) из лабораторной работы 1.
1.  = (2,2) = (2,2)
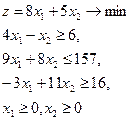
| 2.  = (4,9) = (4,9)
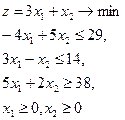
|
3.  = (5,6) = (5,6)
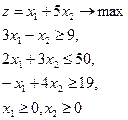
| 4.  = (3,3) = (3,3)
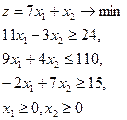
|
5.  = (10,4) = (10,4)
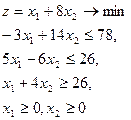
| 6.  = (7,5) = (7,5)
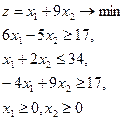
|
7.  = (16,9) = (16,9)
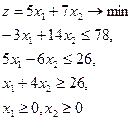
| 8.  = (8,5) = (8,5)
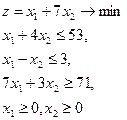
|
9.  = (5,6) = (5,6)
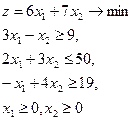
| 10.  = (7,10) = (7,10)
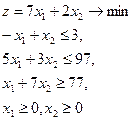
|
11.  = (2,2) = (2,2)
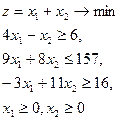
| 12.  = (6,3) = (6,3)
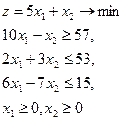
|
13.  = (4,4) = (4,4)
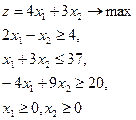
| 14.  = (6,4) = (6,4)
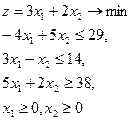
|
15.  = (3,3) = (3,3)
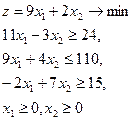
| 16.  = (2,6) = (2,6)
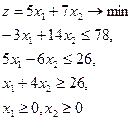
|
17.  = (13,8) = (13,8)
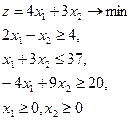
| 18.  = (5,12) = (5,12)
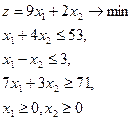
|
19.  = (7,5) = (7,5)
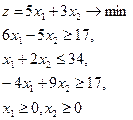
|
20.  = (9,13) = (9,13)
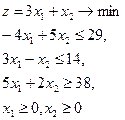
|
21.  = (5,6) = (5,6)
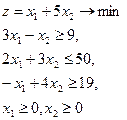
| 22.  = ( = (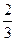 , , 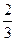 ) )
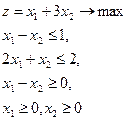
|
23.  = (10,5) = (10,5)
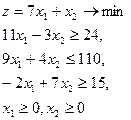
| 24.  = (13,8) = (13,8)
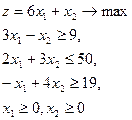
|
25.  = (13,9) = (13,9)
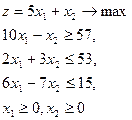
| 26.  = (16,9) = (16,9)
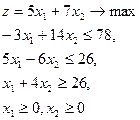
|
 2015-07-14
2015-07-14 373
373








