Теорема. Если при переходе через точку 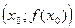
вторая производная меняет знак, то эта точка является точкой перегиба.
Пример 48.1. Рассмотрим функцию 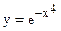 из примера 47.1. Т.к. левее точки
из примера 47.1. Т.к. левее точки 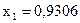 вторая производна
вторая производна 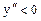 , а правее
, а правее 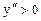 (см. рис. 47.1), то точка
(см. рис. 47.1), то точка 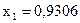 является точкой перегиба. Аналогичные рассуждения можно провести для критических (по второй производной) точек
является точкой перегиба. Аналогичные рассуждения можно провести для критических (по второй производной) точек 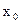 и
и 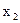 .
.
 2015-07-14
2015-07-14 308
308








