 Сложение векторов
Сложение векторов
 Суммойдвух векторов
Суммойдвух векторов 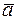 и
и 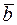 называется третий вектор
называется третий вектор 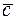 , начало которогосовпадает с началом вектора
, начало которогосовпадает с началом вектора 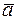 , а конец
, а конец 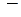 с концом вектора
с концом вектора 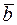 при условии, что вектор
при условии, что вектор 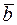 приложен к концу вектора
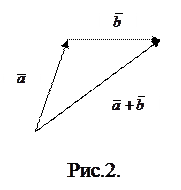
приложен к концу вектора 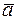 (правило треугольника) (Рис. 2). Тогда
(правило треугольника) (Рис. 2). Тогда
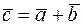
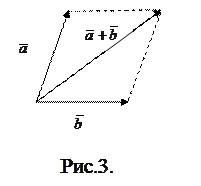 Наряду с правилом треугольника часто пользуются равносильным ему правилом параллелограмма: если векторы
Наряду с правилом треугольника часто пользуются равносильным ему правилом параллелограмма: если векторы 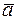 и
и 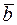 приведены к общему началу и на них построен параллелограмм, то сумма
приведены к общему началу и на них построен параллелограмм, то сумма 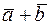 есть вектор, совпадающий с диагональю этого параллелограмма, идущий из общего начала векторов
есть вектор, совпадающий с диагональю этого параллелограмма, идущий из общего начала векторов 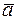 и
и 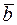 (Рис.3).
(Рис.3).
Сложение векторов подчиняется основным законам сложения чисел:
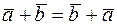 ,
, 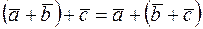 .
.
 Эти свойства позволяют определить сумму любого числа слагаемых по правилу замыкающего вектора, при этом слагаемые можно перемещать и группировать произвольным образам.
Эти свойства позволяют определить сумму любого числа слагаемых по правилу замыкающего вектора, при этом слагаемые можно перемещать и группировать произвольным образам.
Разностью векторов 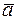 и
и 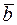 называется третий вектор
называется третий вектор 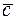 , который в сумме с вектором
, который в сумме с вектором 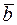 даёт вектор
даёт вектор 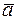 .
.
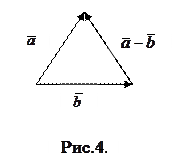
Если два вектора приведены к общему началу, то их разность 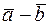 есть вектор, идущий из конца «вычитаемого» к началу «уменьшаемого» вектора (Рис. 4).
есть вектор, идущий из конца «вычитаемого» к началу «уменьшаемого» вектора (Рис. 4).
 Умножение вектора на число
Умножение вектора на число
Произведением вектора 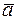 и числа
и числа 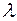 называется вектор
называется вектор 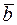 , который коллинеарен вектору
, который коллинеарен вектору 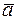 , имеет длину равную
, имеет длину равную 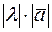 , сонаправлен с вектором
, сонаправлен с вектором 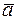 , если
, если 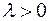 , и противоположнонапровлен, если
, и противоположнонапровлен, если  . Если
. Если 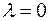 или
или 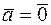 , то
, то 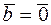 . Обозначается
. Обозначается 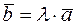
Геометрический смысл операции умножения вектора 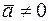 на число
на число 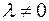 можно выразить следующим образом: если
можно выразить следующим образом: если 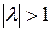 , то вектор
, то вектор 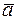 «растягивается» в
«растягивается» в 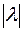 раз, если
раз, если 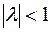 , то «сжимается» в
, то «сжимается» в 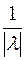 раз. При
раз. При 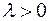 направление не меняется, при
направление не меняется, при  направление меняется на противоположное.
направление меняется на противоположное.
Из определения следует, что 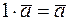 ,
, 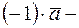 вектор противоположный вектору
вектор противоположный вектору 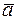 . Обозначим его
. Обозначим его 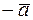 .
.
 2015-07-14
2015-07-14 469
469








