Пусть в пространстве задана ПДСК 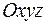 и произвольный вектор
и произвольный вектор 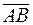 . Пусть, далее,
. Пусть, далее, 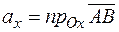 ,
, 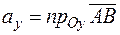 ,
, 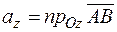 . Проекции
. Проекции 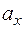 ,
, 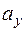 ,
, 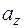 вектора
вектора 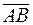 на оси координат называются его координатами. При этом пишут
на оси координат называются его координатами. При этом пишут
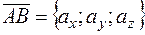 .
.
Если заданы координаты точек 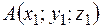 и
и 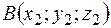 , то координаты вектора
, то координаты вектора
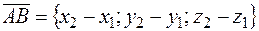 . (5)
. (5)
Следовательно, модуль вектора
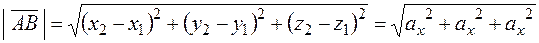 . (6)
. (6)
Пусть 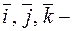 единичные векторы осей координат. Тройка векторов
единичные векторы осей координат. Тройка векторов 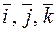 называется базисом.
называется базисом.
Каким бы ни был вектор 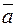 он всегда может быть разложен по базису векторов
он всегда может быть разложен по базису векторов 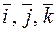 , т.е. может быть представлен в виде:
, т.е. может быть представлен в виде:
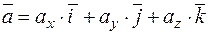 .
.
Коэффициенты этого разложения являются координатами вектора 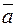 . Если
. Если 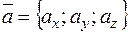 и
и 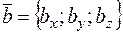 , то
, то
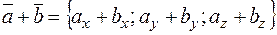 ,
,
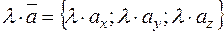 .
.
Два вектора коллинеарны тогда и только тогда когда их координаты пропорциональны:
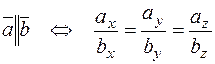 .
.
 2015-07-14
2015-07-14 450
450








