Унімодальні функції

Якщо на відрізку [a,b] визначена функція f(x) з одною точкою локального мінімуму 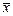і при цьому для всіх 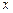< 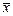функція строго убуває, 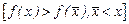, а для всіх 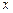> 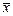функція строго зростає 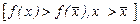, то така функція називається унімодальною.

Обумовленість задачі мінімізації

Похибка визначення точки мінімуму 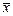пов'язана з граничною абсолютною похибкою обчислення значення функції в точці 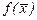наступним чином:

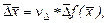(5.4)

де 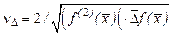- число обумовленості задачі мінімізації. Звідси випливає, що похибка при визначенні x збільшується в 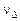у порівнянні з похибкою обчислення функції 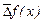. Оскільки при 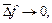маємо 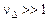, то задача мінімізації є погано обумовленою.