Пример 8. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол 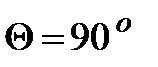 . Энергия
. Энергия 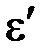 рассеянного фотона равна 0,4 МэВ. Определить энергию
рассеянного фотона равна 0,4 МэВ. Определить энергию 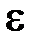 фотона до рассеяния.
фотона до рассеяния.
Решение. Для определения энергии первичного фотона воспользуемся формулой Комптона в виде
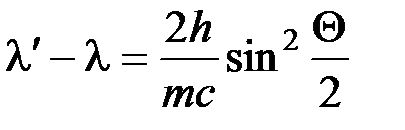 . (8.1)
. (8.1)
Формулу (8.1) преобразуем следующим образом:
1) выразим длины волн 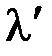 и
и 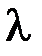 через энергию
через энергию 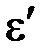 и
и 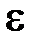 соответствующих фотонов, воспользовавшись соотношением
соответствующих фотонов, воспользовавшись соотношением 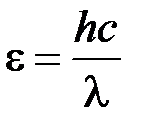 ;
;
2) умножим числитель и знаменатель правой части формулы на с.
Тогда получим
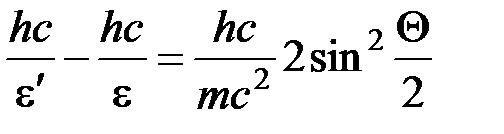 .
.
Сократив на 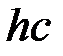 , выразим из этой формулы искомую энергию:
, выразим из этой формулы искомую энергию:
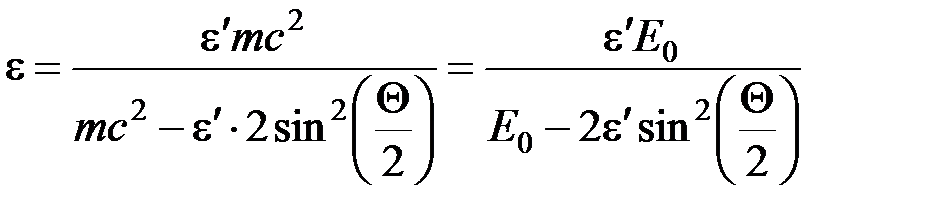 , (8.2)
, (8.2)
где 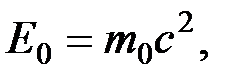 где
где 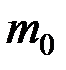 - масса покоя электрона.
- масса покоя электрона.
Вычисления по формуле (8.2) удобнее вести во внесистемных единицах. Взяв значение энергии покоя электрона 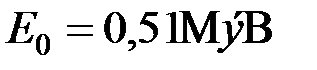 и подставив числовые данные, получим
и подставив числовые данные, получим
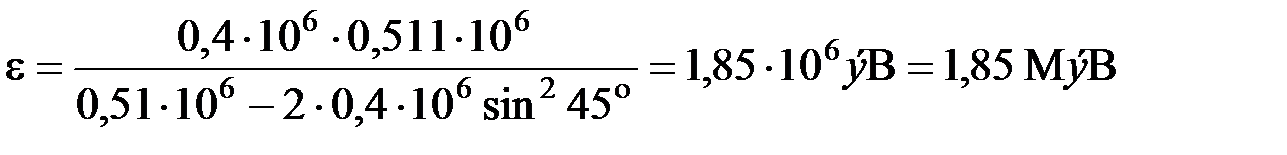 .
.
Ответ: энергия фотона до рассеяния равна 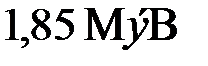 .
.
Атом водорода.
Пример 9. Определить энергию E фотона, соответствующую второй линии в серии Лаймана атома водорода.
Решение. Энергия Е фотона, излучаемого атомом водорода при переходе электрона с одной орбиты на другую:
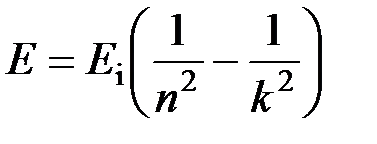 ,
,
где 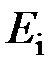 – энергия ионизации атома водорода, (
– энергия ионизации атома водорода, (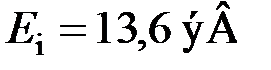 ); n = 1, 2, 3,… - номер орбиты, на которую переходит электрон; k=n +1; n +2; …; n+m – номер орбиты, с которой переходит электрон; m – номер спектральной линии в данной серии.
); n = 1, 2, 3,… - номер орбиты, на которую переходит электрон; k=n +1; n +2; …; n+m – номер орбиты, с которой переходит электрон; m – номер спектральной линии в данной серии.
Для серии Лаймана n =1, для второй линии этой серии m =2, тогда k=n+m =1+2=3.
Поставив числовые значения, найдем энергию фотона: Е =12,09 эВ.
Ответ: энергию фотона Е =12,09 эВ.
Пример 10. Определите, какую ускоряющую разность потенциалов 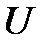 должен пройти протон, чтобы длина волны де Бройля для него была равна λ=1 нм.
должен пройти протон, чтобы длина волны де Бройля для него была равна λ=1 нм.
Решение. Протон, прошедший ускоряющую разность потенциалов 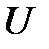 , приобретает кинетическую энергию
, приобретает кинетическую энергию 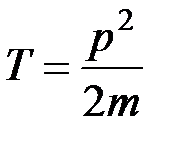 , которая равна
, которая равна 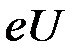 . Отсюда
. Отсюда
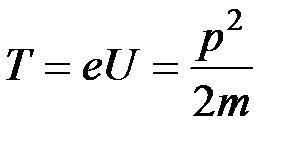 ,
,
где 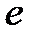 – заряд протона;
– заряд протона; 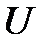 – ускоряющая разность потенциалов;
– ускоряющая разность потенциалов; 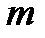 – масса протона;
– масса протона; 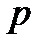 – величина импульса протона.
– величина импульса протона.
Откуда 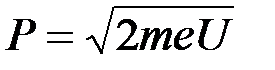 .
.
Длина волны де Бройля 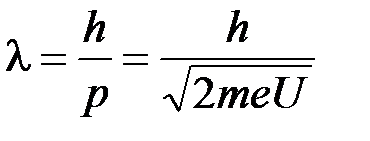 ,
,
где 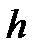 – постоянная Планка,
– постоянная Планка,
и 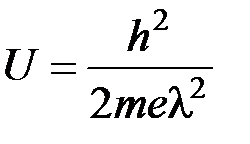 .
.
Произведем вычисления:
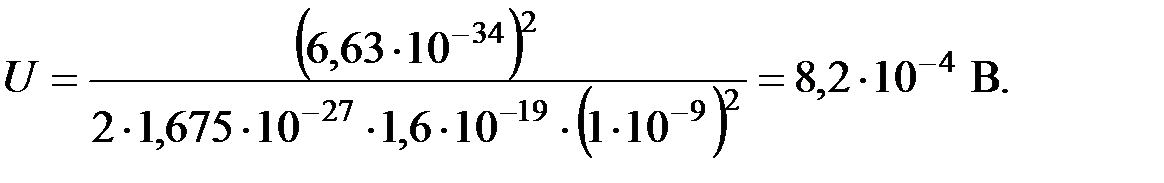
Ответ: ускоряющая разность потенциалов 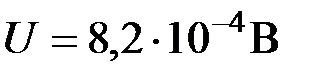 .
.
 2015-07-14
2015-07-14 1527
1527








