Теорема (Коши).
Для того, чтобы у функции 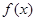 , определенной в интервале
, определенной в интервале 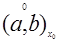 , существовал придел необходимо и достаточно, чтобы выполнялось условие:
, существовал придел необходимо и достаточно, чтобы выполнялось условие: 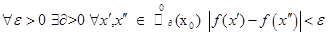
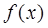 опр. на
опр. на 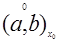
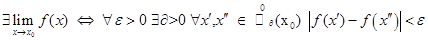
Доказательство.
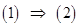
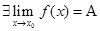 ,тогда фиксируем произвольную
,тогда фиксируем произвольную 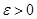 . Для этой зафиксированной
. Для этой зафиксированной 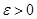
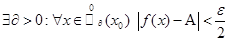 . Таким образом
. Таким образом  имеем,что
имеем,что 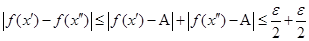 .
.
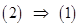
Рассмотрим 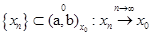 . Раз это так, то верным является, что
. Раз это так, то верным является, что 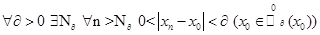 . По условию
. По условию 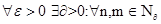 выполняется, что
выполняется, что  . Таким образом,
. Таким образом, 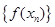 является фундаментальной
является фундаментальной 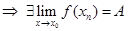 .
.
Докажем, что A не зависит от выбора последовательности. Рассмотрим любую другую последовательность  .И пусть,
.И пусть, 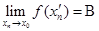 ,посмотрим, будет ли A=B. Смешаем два последовательности так, что на четных местах одна, а на нечетных другая:
,посмотрим, будет ли A=B. Смешаем два последовательности так, что на четных местах одна, а на нечетных другая: 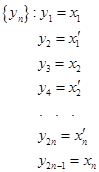 .
. 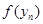 -фундаментальная, так как смешали две фундаментальные последовательности и
-фундаментальная, так как смешали две фундаментальные последовательности и 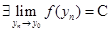 ,но последовательность
,но последовательность 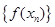 - подпоследовательность
- подпоследовательность 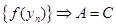 ; а последовательность
; а последовательность 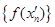 - подпоследовательность
- подпоследовательность 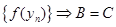 .И из этого следует, что
.И из этого следует, что 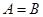 .
.
 2015-07-14
2015-07-14 264
264







