Определение.
Функции 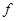 и
и 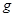 определены в интервале
определены в интервале 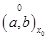 ,если
,если 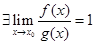 ,то будем говорить, что
,то будем говорить, что 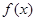 эквивалентна
эквивалентна 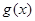 и писать:
и писать: 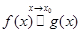 .
.
Важнейшие эквивалентности при 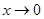 :
:
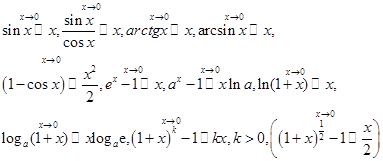
Определение.
Если 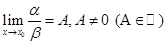 ,то
,то 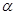 и
и 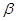 называются бесконечно-малыми одного порядка. Если
называются бесконечно-малыми одного порядка. Если 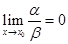 ,то
,то 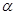 называется бесконечно-малой более высокого порядка, чем
называется бесконечно-малой более высокого порядка, чем 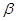 . Если
. Если 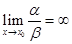 ,то
,то 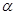 называется бесконечно-малой более низкого порядка, чем
называется бесконечно-малой более низкого порядка, чем 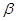 .Если
.Если 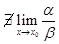 ,значит
,значит 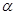 и
и 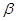 называются несравнимыми бесконечно-малыми.
называются несравнимыми бесконечно-малыми.
Пример.
1) 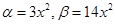 при
при 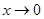
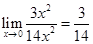 ,
, 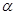 и
и 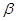 называется бесконечно-малыми одного порядка, то есть стремятся к 0 с одинаковой скоростью.
называется бесконечно-малыми одного порядка, то есть стремятся к 0 с одинаковой скоростью.
2) 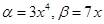 при
при 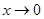
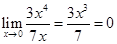 -более высокого порядка, значит
-более высокого порядка, значит 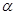 стремится к 0 быстрее, чем
стремится к 0 быстрее, чем 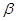 .
.
 2015-07-14
2015-07-14 183
183







