Основы теории пассивного эксперимента

Разработка уравнения регрессии включает в себя две задачи: разработка формы уравнения регрессии и расчет коэффициентов уравнения регрессии В.

При обработке выборки экспериментальных данных для однопараметрической зависимости 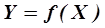используют графический метод поиска формы уравнения регрессии. При этом часто возникают ситуации, когда набор опытных точек может быть описан несколькими вариантами уравнения регрессии. Так, например, для случая, рассмотренного на рис. 3.2 можно предложить три варианта уравнения регрессии:

линейное уравнение

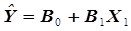, (3.8)

квадратичное уравнение

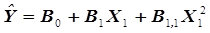, (3.9)

кубическое уравнение

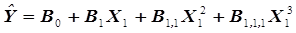. (3.10)

3 1 2

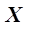
Рис. 3.2. К выбору формы уравнения регрессии

1 – линейная, 2 – квадратичная, 3 - кубическая

Обычно при поливариантном подходе к выбору формы уравнения регрессии разработку уравнения начинают с простейшей формы (например, линейной), что позволяет сократить объем расчетов при определении коэффициентов уравнения регрессии и последующем многократном использования уравнения как модели при математическом моделировании процесса, а если впоследствии эта форма уравнения окажется неприемлемой (неадекватной), то переходят к более сложным формам уравнения регрессии.

В тех случаях, когда имеющаяся выборка экспериментальных данных достаточно четко свидетельствует о наличии ряда экстремумов (максимумов и минимумов) (рис. 3.3), то уравнение регрессии имеет порядок по крайней мере на единицу больший, чем число экстремумов. Например, для зависимости 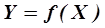, приведенной на рис 3.3 и имеющей пять экстремумов уравнение регрессии имеет вид

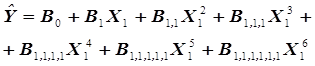. (3.11)

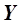
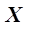
Рис. 3.3. К выбору порядка уравнения регрессии

В тех случаях, когда уравнение регрессии является функцией нескольких переменных из общего набора экспериментальных данных формируют выборки, характеризующие влияние одного из параметров на результат процесса при постоянстве остальных параметров процесса. Например, для зависимости 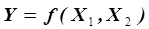составляют выборки 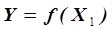при постоянстве 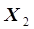м 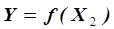при постоянстве 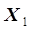(рис.3.4), подбирая форму уравнения регрессии для каждой из частных зависимостей. В примере, приведенном на рис. 3.4, 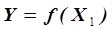является линейной:

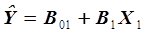, (3.12)

а функция 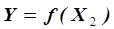является квадратичной:

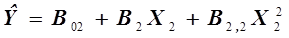. (3.13)

Итоговое уравнение регрессии получают суммированием уравнений (3.12) и (3.13)

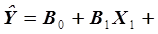
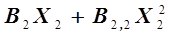. (3.14)

Недостатком уравнения регрессии (3.14) является отсутствие в нем возможного эффекта взаимодействия, который вводится в уравнение (3.14) дополнительно, приводя к форме

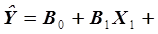
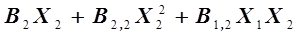. (3.15)

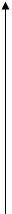
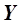
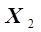=const.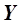 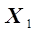= const.

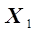
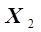
а б

Рис. 3.4. Формирование частных выборок при разработке двухпараметрической зависимости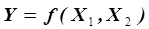

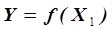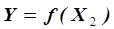(а) и (б)

Часто при разработке многопараметрических уравнений регрессии на основе частных уравнений применяют метод Брандона, при котором общее уравнение регрессии есть произведение частных уравнений, например, для выше рассмотренной задачи метод Брандона дает следующее уравнение регрессии:

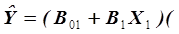
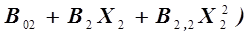, (3.16)

которое после перемножения выражений в скобках и приведения подобных членов принимает форму

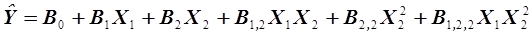. (3.17)

Расчет коэффициентов уравнения регрессии обычно выполняют методом наименьших квадратов, при этом численные значения коэффициентов должны быть такими, чтобы разница между опытными 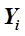и расчетными 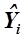(по уравнению регрессии) данными в сходственных точках (то есть при одинаковых значениях параметров 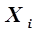были минимальными по всему объему экспериментов 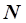. Функция наименьших квадратов имеет в общем случае вид

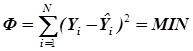. (3.18)

Численные значения коэффициентов, удовлетворяющие требованию минимизации (3.18) находят, решая систему уравнений из частных производных функции Ф, которые равны нулю.

Например, для уравнения регрессии 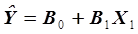функция Ф имеет вид

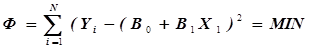(3.19)

и условию ее экстремума соответствует система уравнений

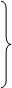
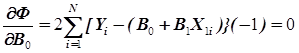
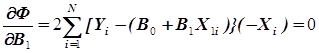, (3.20)

дающая после преобразований систему линейных алгебраических уравнений

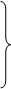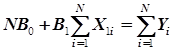
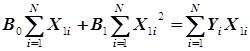, (3.21)

решаемую методами Гаусса или Крамера [13].

Таким образом, уравнение регрессии позволяет в компактной форме систематизировать экспериментальные данные, подвергнуть при наличии математической модели исследуемый процесс аналитическому исследованию, ввести систематизированные справочные данные в дальнейший расчет и т.д.

Рассмотрим пример разработки уравнения регрессии как составной части математической модели. Пусть при расчете процесса окисления изопропилбензола в барботажном реакторе потребуется использовать зависимость поверхностного натяжения изопропилбензола s от температуры для моделирования работы барботера при различных температурах процесса t. По справочнику [14]найдем следующие исходные данные (табл.3.1):

Таблица 3.1