2015-07-14
877
Поскольку стохастические модели представляют собой формальные алгебраические уравнения, разработанные на основе экспериментальных данных, то, в отличие от детерминированных моделей, эти модели можно получать на базе единых принципов для любых задач моделирования.
Стохастические алгебраические модели чаще всего формируют в виде степенных зависимостей, когда параметр процесса Х выступает в качестве основания степени, например,
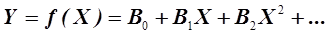(3.1)
Подобного рода уравнения часто называют уравнением регрессии. Регрессией в общем случае называется истинное изменение величины одного из выходных параметров системы (например,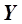 
) при изменении вектора входных параметров 
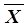. Поскольку в ходе эксперимента мы получаем не истинные значения 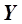, а случайные 
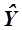, и, кроме того бесконечный полином (3.1) ограничивают некоторым членом, внося погрешность в расчет 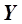, то эквивалентом (3.1) в качестве приближенной регрессии является уравнение вида
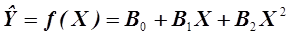. (3.2)
Докажем правомочность использования формального полиномиального уравнения регрессии в качестве математической модели изучаемого процесса. Из теории рядов известно, что любую непрерывную и дифференцируемую функцию (а именно из подобных выражений формируются детерминированные модели)
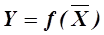, (3.3)
которую сложно, а порой невозможно рассчитать аналитически, можно разложить в бесконечный ряд, например, Тейлора:
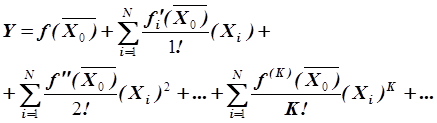, (3.3)
где i =1, 2, …, N – число параметров Х, К – порядок производной.
Так как ряд Тейлора сходится, то можно оборвать ряд на любом члене разложения и рассчитать сумму членов остатка бесконечного ряда, характеризуя ею погрешность расчета 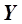с применением теории рядов.
Производные в ряде Тейлора (3.3) можно интерпретировать как численные значения коэффициентов бесконечного полинома
, (3.4)
в котором 
эквивалентны первым производным,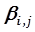 
эквивалентны смешанным парным производным, 
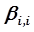эквивалентны вторым производным и т.д. и имеют с позиций математической статистики смысл генеральных оценок, то есть наиболее достоверных численных значений коэффициентов 
. Нетрудно увидеть, что уравнение (3.4) является полиномом. В отличии от ряда (3.4), конечное уравнение регрессии не позволяет рассчитать погрешность расчета в виде суммы членов недостающей части бесконечного полинома, что и приводит к погрешности расчета 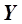по уравнению регрессии, эквивалентному (3.4) и записанному в виде:
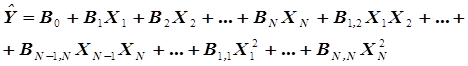, (3.5)
так как в ходе обработки экспериментальных данных рассчитываются не генеральные оценки 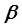, а их вероятностные оценки В, величина которых зависит от числа опытных данных и погрешности измерений в эксперименте, то есть значения В имеют вероятностный характер. Уясним эту ситуацию на простом примере.
Допустим, что разрабатывается зависимость
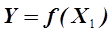, (3.6)
которая является линейной, тогда она может быть описана уравнением прямой линии
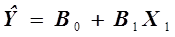. (3.7)
Для расчета коэффициентов 
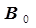и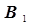 
достаточно провести два опыта с определением 
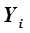при двух значениях 
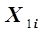. Опытные точки отложены на рис. 3.1 в виде. Для расчета 
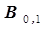необходимо отложить отрезок на оси 
при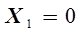 
; для расчета 
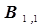необходимо рассчитать тангенс угла наклона прямой 
.
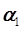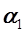
В0,1 В0,2
0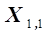 
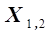
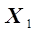
Рис. 3.1. К обоснованию вероятностного характера
коэффициентов уравнения регрессии
Допустим, что усомнившись в качестве выполненного эксперимента мы решили его повторить, при этом новые точки располагаются на рис. 3.1 достаточно близко от старых точек, то есть погрешность эксперимента невысока, что субъективно свидетельствует о неплохом качестве экспериментов. 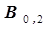Однако, если мы представим себе, что вторая выполненная серия опытных точек является в эксперименте единственной, то рассчитанные значения коэффициентов уравнения регрессии 
и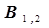 
будут отличаться от ранее рассчитанных для первой серии опытов коэффициентов 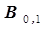и 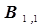. Если же мы попытаемся учесть для расчета коэффициентов уравнения регрессии все четыре опыта, то получим новые варианты значений коэффициентов 
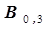и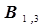 
.Таким образом численные значения коэффициентов уравнения регрессии зависят от числа опытных точек и погрешности эксперимента.
Различные группы членов уравнения регрессии (3.5) имеют различный стохастический смысл. Свободный член 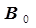характеризует величину параметра 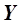при равенстве нулю всех входных параметров 
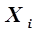; линейные члены уравнения 
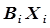характеризуют тесноту связи 
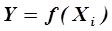, квадратичные члены уравнения 
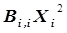характеризуют отклонение зависимости 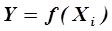от линейного закона. Особый интерес вызывают включаемые в уравнение регрессии члены, представляющие собой эффекты взаимодействия типа 
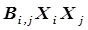, характеризующие совместное влияние двух и более параметров системы 
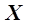на результат процесса 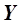и приводящие к нарушению закона аддитивности. Примером наличия эффекта взаимодействия могут служить сплавы, например бронза, у которой твердость сплава выше твердости исходных компонентов, или азеотропные растворы, температура которых ниже или выше температур кипения компонентов раствора. Эффекты взаимодействия для 
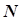-факторной задачи по всей совокупности факторов могут быть парными (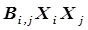), тройными (
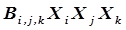), четверными (
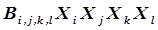) и так далее до достижения 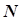-мерного эффекта взаимодействия. 
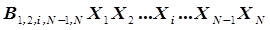. Индексация коэффициентов В соответствует индексам параметров в рассматриваемом слагаемом, например, 
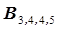соответствует слагаемому уравнения регрессии 
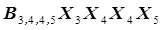или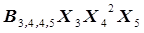 
. Поскольку априорно неизвестно, какие эффекты взаимодействия реально существуют в моделируемом процессе, то при формировании уравнения регрессии в него включают все теоретически возможные варианты эффектов взаимодействия, что существенно увеличивает объем стохастической модели. Так, например, для 10-факторной задачи при разработке линейного уравнения регрессии оно будет включать 1024, в том числе один свободный член, 10 линейных членов и 1013 членов, характеризующих различные наборы эффектов взаимодействия от многочисленных парных эффектов до единственного десятерного эффекта взаимодействия.
При разработке стохастических моделей различают исходный пассивный и активный эксперименты.
При пассивном эксперименте разработчик модели использует независимый от него набор исходных опытных точек, полученных в произвольном эксперименте, по справочным таблицам или в результате обследования промышленных объектов, когда по материалам записей вахтового операторного журнала за большой период времени набирают информацию о поведении параметра 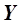при варьировании параметров , формируя экспериментальную выборку.
При активном эксперименте разработчик модели участвует в формировании выполняемого эксперимента таким образом, чтобы свести к минимуму объем экспериментов и последующей математической обработки опытных данных при расчете коэффициентов уравнения регрессии.
