Метод классического аналитического поиска экстремума

Метод основан на том, что целевая функция

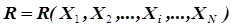= МАХ (5.2)

действительно имеет экстремум, если в точке, подозреваемой на наличие экстремума, производные 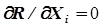(необходимое условие экстремума) и в окрестности точки, подозреваемой на наличие экстремума, меняется знак производной 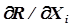(достаточное условие). Таким образом, решение задачи сводится к формированию системы уравнений

…

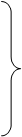
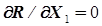
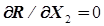
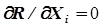, (5.3)

…

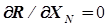
решение которой дает оптимальные значения параметров .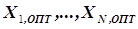

Классический аналитический метод поиска экстремума обычно применяют, когда формирование уравнений 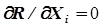не представляет труда и решение системы уравнений (5.3) достаточно несложно.

В качестве примера применения метода рассмотрим задачу об определении оптимальных условий реализации химической реакции.