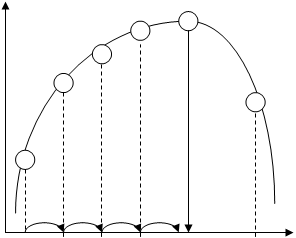
Простейшим из безградиентных методов является метод сканирования (рис 5.3). Алгоритм расчета при исходных данных (целевая функция – 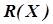 = МАХ, область исследования –
= МАХ, область исследования – 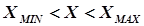 , погрешность определения точки экстремума –
, погрешность определения точки экстремума – 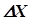 ) заключается в сканировании (прохождении) оси Х в интервале от
) заключается в сканировании (прохождении) оси Х в интервале от 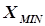 до
до 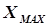 с шагами
с шагами 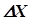 и расчетом значения критерия
и расчетом значения критерия 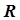 по целевой функции
по целевой функции 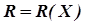 с запоминанием лучшего результата оптимизации.
с запоминанием лучшего результата оптимизации.
|
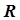
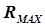 Реализация алгоритма следующая:
Реализация алгоритма следующая:
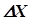
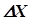
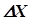
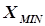 Х1 Х2 Х3
Х1 Х2 Х3 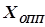
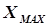 Х
Х
Рис. 5.3. Иллюстрация метода
сканирования
В рассмотренном алгоритме в памяти содержится характеристика глобального экстремума целевой функции (рис.5.1). Если целевая функция содержит один экстремум, то в пункте 5 алгоритма вводится условие прекращения сканирования и, соответственно, решения задачи в виде: если
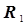
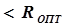 , то расчет прекращают.
, то расчет прекращают.
Метод сканирования – это единственный из методов нелинейного программирования, позволяющий рассчитать глобальный экстремум. Недостатком метода является длительность решения задачи в связи с необходимостью выполнения большого числа циклов расчета 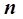 :
:
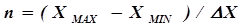 , (5.28)
, (5.28)
так, например, если Х – это температура процесса, исследуемая в интервале 100-400 0С с шагом 0.5 0С, то для решения задачи будет необходимо выполнить 600 циклов расчета.
Намного эффективнее метода сканирования при наличии единственного экстремума методы локализации экстремума, в частности, метод чисел Фибоначчи. В этом методе шаги в области исследования по оси выполняются пропорционально числам Фибоначчи (табл. 5.1), которые рассчитываются по рекуррентному соотношению
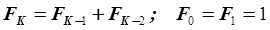 . (5.29)
. (5.29)
Как следует из табл. 5.1, числа Фибоначчи резко возрастают с увеличением их порядкового номера.
Таблица 5.1
Числа Фибоначчи
| Порядковый номер к | |||||||
Числа Фибоначчи 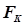
| |||||||
| Порядковый номер к | |||||||
Числа Фибоначчи 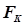
| |||||||
| Порядковый номер к | |||||||
Числа Фибоначчи 
|
Если заданы целевая функция 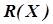 = МАХ, область исследования
= МАХ, область исследования 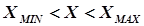 и погрешность определения точки экстремума –
и погрешность определения точки экстремума – 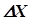 , то методом чисел Фибоначчи необходимо выполнить к циклов расчета, где к – порядковый номер ближайшего числа Фибоначчи, большего числа циклов при решении задачи методом сканирования:
, то методом чисел Фибоначчи необходимо выполнить к циклов расчета, где к – порядковый номер ближайшего числа Фибоначчи, большего числа циклов при решении задачи методом сканирования:
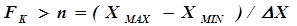 . (5.30)
. (5.30)
Так, например, если в примере, приведенном на стр. 126 число циклов расчета методом сканирования составляло 600, то при ближайшем большем числе Фибоначчи 610 (табл. 5.1) рассматриваемым методом придется выполнить лишь 14 циклов расчета.
Алгоритм расчета включает следующие этапы:
1. Определяется минимальный шаг поиска экстремума
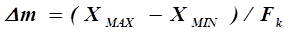 , (5.31)
, (5.31)
очевидно, что 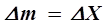 , если
, если 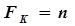 , и
, и 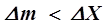 , если
, если 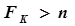 .
.
2. Вычисляется величина 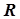 в точке
в точке 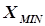 .
.
3. Выполняется переход из точки 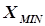 в точку Х1 с координатой
в точку Х1 с координатой
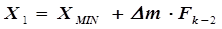 (5.32)
(5.32)
и в этой точке рассчитывается величина критерия 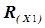 .
.
4. Если шаг оказался удачным (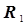 больше
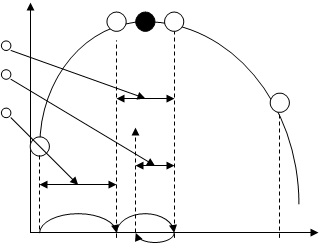
больше 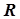 ), т следующий шаг выполняется в том же направлении, что и предыдущий, но с последовательным уменьшением числа Фибоначчи на каждом шаге. На рис. 5.4 первый шаг – удачен и выполнен переход в точку
), т следующий шаг выполняется в том же направлении, что и предыдущий, но с последовательным уменьшением числа Фибоначчи на каждом шаге. На рис. 5.4 первый шаг – удачен и выполнен переход в точку
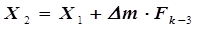 . (5.33)
. (5.33)
Если шаг оказался неудачным, то меняется направление движения к экстремуму и переходим последовательно в новые точки, каждый раз уменьшая число Фибоначчи. На рис. 5.4 второй шаг оказался неудачным и координаты очередной третьей точки нашли как
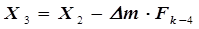 . (5.34)
. (5.34)
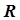
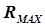
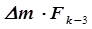
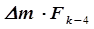
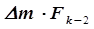
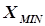 Х1 Х3Х2
Х1 Х3Х2 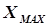 Х
Х
Рис. 5.4. Иллюстрация метода чисел Фибоначчи
Процесс пошагового расчета выполняется до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности, при этом последнее число Фибоначчи 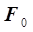 обеспечивает шаг
обеспечивает шаг
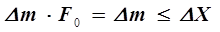 , (5.35)
, (5.35)
то есть оно определяет координаты экстремума с заданной степенью точности или выше ее.
 2015-07-14
2015-07-14 546
546

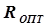 , ХОПТ.
, ХОПТ.  5. Продолжается сканирование оси Х по пунктам 2-4 алгоритма до достижения Х =
5. Продолжается сканирование оси Х по пунктам 2-4 алгоритма до достижения Х = 






