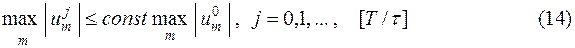Начально-краевые задачи для уравнения гиперболического типа (волнового уравнения)

1.1. Задание. Найти численное решение задачи вида

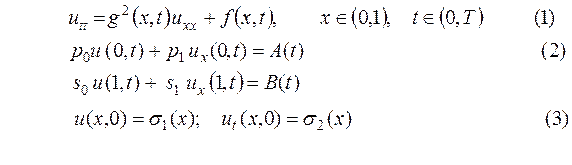1) при помощи явной схемы МКР;

2) при помощи неявной схемы МКР.

Найти решение с точностью до 0.0001 на отрезке времени 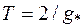, где 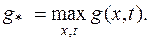При использовании явной схемы предварительно определить условие ее устойчивости. При помощи средств пакета Maple построить графики функций u(x_*,t), u(x,jt_*), где x_* =0.6, t_* = T/4, j= 1,2,3. Сравнить результаты, полученные по явной и по неявной схемам МКР. Проверить правильность работы программы на тестовом примере

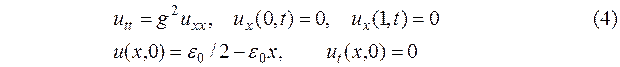
Точным решением задачи является ряд

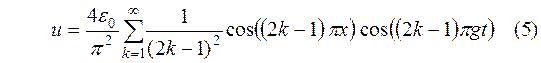
Расчет провести при следующих значениях параметров: g=const= 1; e₀= 0.02.

Рекомендуемая литература:

1.2. Идея МКР.

Для решения задачи при помощи МКР стремятся построить такие разностные схемы, которые бы обеспечивали сходимость получаемого решения разностной задачи к решению исходной дифференциальной при измельчении сетки. В 16.1 сформулирована теорема о том, “что если разностная краевая задача аппроксимирует дифференциальную задачу и устойчива, то при измельчении сетки решение разностной задачи сходится к решению дифференциальной”. Из этого следует, что для получения нужной схемы необходимо строить аппроксимирующие разностные схемы и выбирать среди них устойчивые.

1.3. Построение явной разностной схемы.

На примере решения задачи (4) рассмотрим один из простейших приемов построения аппроксимирующей разностной схемы. Он связан с заменой производных приближенными разностными соотношениями:

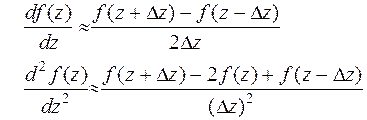(6)

Используя разложения функции f(z) в ряд Тейлора в окрестности точки z, легко показать, что первая и вторая производные аппроксимируются формулами (6) с точностью до членов порядка (Dz)². Аналогичные формулы используем и для замены частных производных в задаче (4).

В качестве сетки, на которой будем рассматривать задачу (4), используем совокупность точек пересечения прямых x= ih, t= jt, i= 0, 1,..., [1 /h ]; j= 0, 1,..., [ T/t ], где h и t - расстояния (шаги) между соседними узлами сетки соответственно по пространственной и временной координатам, [ T/t ] - целая часть числа T/t (рис.1). Считаем, что шаги h и t связаны соотношением t= rh, r= const, так что сетка зависит только от одного параметра h. Вместо функции u будем искать сеточную функцию, значения которой додлжны сходиться к значениям функции u в узлах при измельчении сетки. Через u_i^j обозначим значение сеточной функции в точке (x_i, t_j) = (ih,jt). На рис.1 сплошными жирными точками изображены реальные узлы сетки, а квадратиками – так называемые фиктивные (или законтурные).

Cетка, на которой решается задача (1)-(3)

t=jt

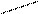
Рис. 1

Разностную схему, отвечающую исходной задаче (4), получим, приблизив производные разностными соотношениями соответственно (6). Например,

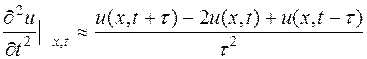
Искомая схема примет вид

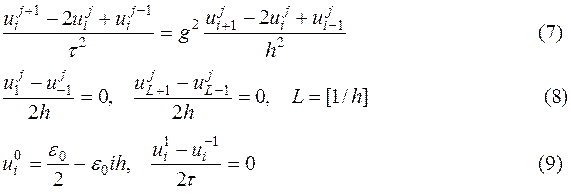
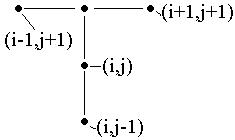
Схеме (7)-(9) отвечает шаблон, изображенный на рис.2 (типа “крест”). Он иллюстрирует тот факт, что для вычисления значения искомой функции на текущем шаге по времени (на временном слое j+1) необходимо знать значения этой функции на двух предыдущих слоях (j и j-1).

Пятиточечный шаблон явной схемы МКР для задачи (1)-(3)

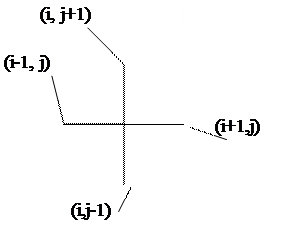Рис. 2

Разрешая уравнение (7) относительно u_i^j+1, находим

Рис.2

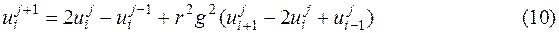
Равенство (10) позволяет явно вычислить значение сеточной функции u_i^j в последовательные моменты времени t_j = jt, j= 0,1,…, а на каждом временном слое – во всех точках x_i=ih, i= 0,1,…, L.Схема, которой отвечает шаблон типа “крест” (см. рис.2), называется явной схемой МКР.

Для того, чтобы запустить вычислительный процесс, требуется исключить из начальных условий (9) значения функции u в законтурных узлах j=-1 (u_i^-1); а для вычисления значений сеточной функции на краях отрезка интегрирования требуется исключить значения функции u в законтурных узлах i=L+1, i=-1 (u_L+1^j и u_-1^j) из граничных условий (8).

Выполнив указанные действия, получим следующие вычислительные формулы

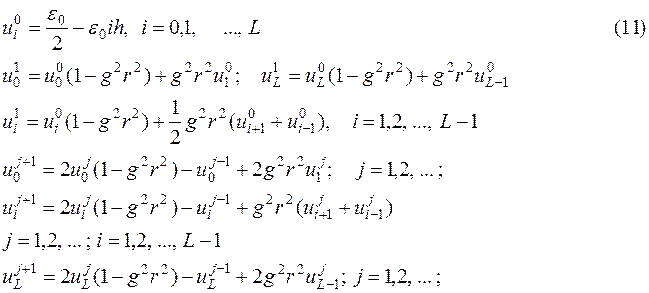
Можно показать, что схема (7)-(9) имеет второй порядок аппроксимации относительно h. Далее, для того, чтобы решение задачи (7)-(9) сходилось к решению исходной задачи, требуется, чтобы эта схема была устойчивой. Рассмотрим один из наиболее популярных методов исследования устойчивости.

1.4. Способ Неймана исследования устойчивости задачи Коши

Рассмотрим задачу Коши

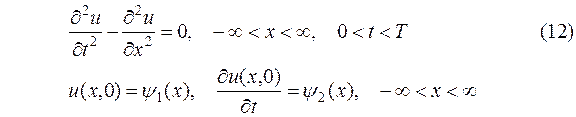
и аппроксимируем ее схемой

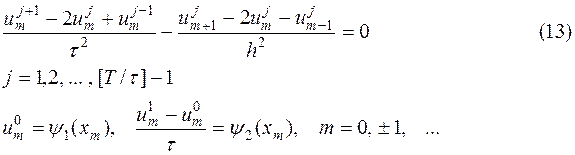
Можно показать (см. [21]), что для устойчивости разностной схемы необходимо, чтобы решение задачи (13) удовлетворяло условию

при произвольной ограниченной функции 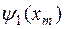, где 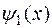задает начальное возмущение решения. Поэтому свойство (14) называют устойчивостью задачи (12) относительно возмущения начальных данных. Для устойчивости задачи Коши (12) по начальным данным необходимо, чтобы условие (14) выполнялось, в частности, и для 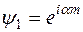, где a - вещественный параметр. Тогда решение задачи (12) можно искать в виде

где 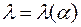определяется путем подстановки (15) в (12). Далее, можно показать, что условие (14) будет выполнено, если числа 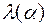(вообще говоря, - комплексные) лежат в единичном круге, т.е. выполняется условие

Неравенство (16) и выражает необходимое условие устойчивости Неймана применительно к рассматриваемому примеру. Используем его для анализа устойчивости схемы (7). Подставим (15) в (7) и для определения 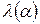получим уравнение

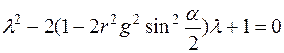(17)

По теореме Виета имеем, что произведение корней этого уравнения равно 1, т.е. для выполнения условия (16) требуется, чтобы корни 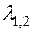уравнения (17) были комплексно-сопряженными и лежали на единичной окружности. Для этого, в свою очередь, необходимо, чтобы дискриминант 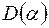уравнения (17) был отрицателен:

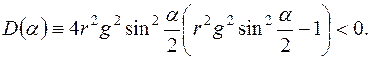
Данное неравенство выполняется при всех a, если 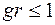. Отсюда следует, что для устойчивости построенной схемы необходимо, чтобы шаг по временной координаты был связан с шагом по пространственной координате неравенством

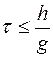(18)

Пусть теперь g=g(x,t)¹ const. В этом случае применяется принцип “замороженных коэффициентов” (см. [21]), в соответствии с которым необходимое условие устойчивости Неймана можно записать в виде

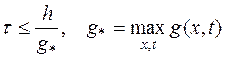(19)

В заключение отметим, что описанный подход применяется и для анализа устойчивости явной конечноразностной схемы, которая строится для соответствующего параболического уравнения. Вопрос влияния граничных условий на устойчивость разностной схемы в настоящих методических указаниях не рассматривается.

1.5. Неявная схема МКР.

В выражении (4) вторая производная ¶²u/¶x² была заменена конечной разностью на временном слое t_j = jt. Если замену провести на временном слое t_j+1 = (j+1)t, то вместо (7) получим

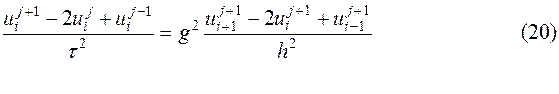Уравнению (20) отвечает шаблон, изображенный на рис.3.

Пятиточечный шаблон неявной схемы МКР для задачи (1)-(3)

Рис.3

Рис. 3

Видно, что из уравнения (20) невозможно явно выразить 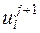через значения функции u с предыдущих слоев по времени (j и j-1). Это происходит оттого, что в (20) наряду с 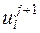входят неизвестные 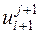и 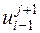. Поэтому данная схема и называется неявной.

Обозначив 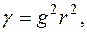перепишем (20) в виде

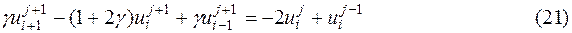
Используя соотношения (8), (9), получим

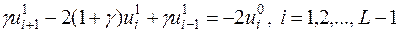	(22)
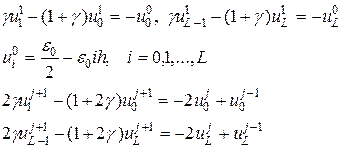	(23) (24) (25) (26)

Опишем по шагам алгоритм решения системы уравнений (21)-(26) с применением метода прогонки.

Шаг первый. Вычисление значений функции u на нулевом слое по времени из уравнений (24).

Шаг второй. Вычисление значений функции u на первом слое по времени из уравнений (22), (23) при помощи метода прогонки. Для применения этого процесса перепишем (22), (23) в стандартном для прогонки виде

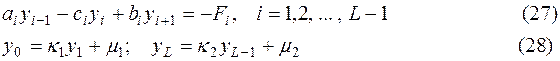
Здесь введены обозначения

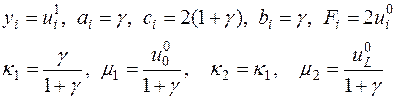(29)

Для возможности применения метода прогонки достаточно потребовать, чтобы коэффициенты системы (27), (28) удовлетворяли условиям

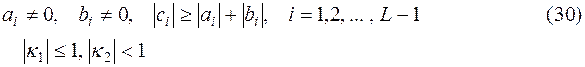
Очевидно, параметры (29) удовлетворяют условиям (30).

Коэффициенты прямой прогонки вычисляем по формулам

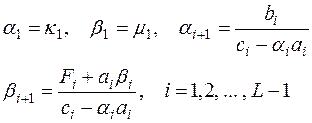(31)

Неизвестные y_i находим в ходе обратной прогонки по формулам

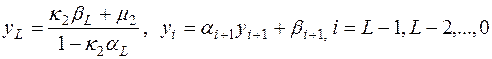(32)

Шаг третий (и последующие). Вычисление значений функции u на (j+1) -ом слое по времени (j ³1) из уравнений (21), (25), (26) в цикле по j при помощи метода прогонки. Для применения этого процесса перепишем (21), (25), (26) в виде (27), (28), введя обозначения

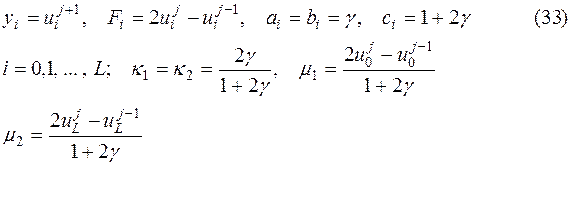Очевидно, что для параметров (33) удовлетворяются условия (30) и, следовательно, здесь также можно применить метод прогонки. Вычисление коэффициентов и неизвестных (последовательно для каждого j = 1,2, …) проводится по формулам (32), (33) аналогично тому, как это описано на Шаге втором.

Отметим, что неявная схема, как говорят, безусловно устойчива, т.е. обеспечивает сходимость разностной задачи к решению соответствующей дифференциальной при любом отношении t/h.