Задача 1
Используя определение производной, найти 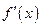 для функции
для функции 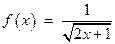 .
.
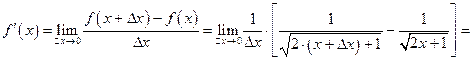
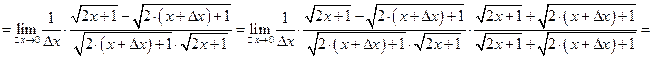
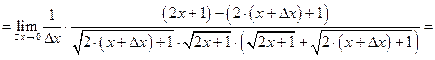
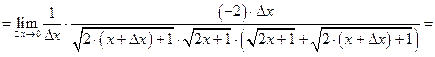
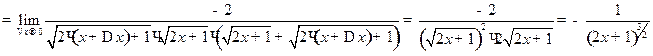 .
.
Задача 2
Найти производные следующих функций:
2.1 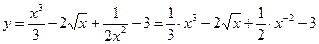 ;
;
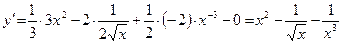 ;
;
2.2 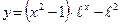 ;
; 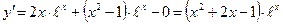 ;
;
2.3 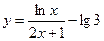 ;
; 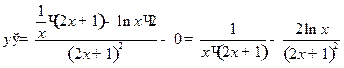 ;
;
2.4 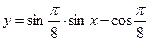 ;
; 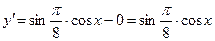 ;
;
2.5 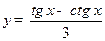 ;
;
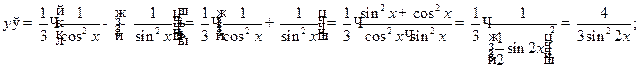
2.6 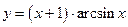 ;
; 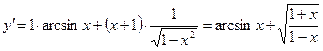 ;
;
2.7 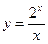 ;
; 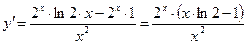 ;
;
2.8 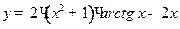 ;
; 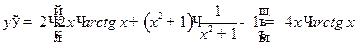 ;
;
2.9 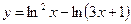 ;
; 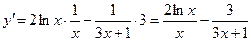 ;
;
2.10 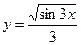 ;
; 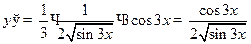 ;
;
2.11 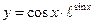 ;
; 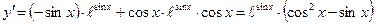 ;
;
2.12 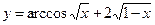 ;
;
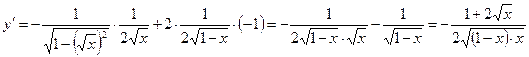 ;
;
2.13 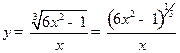 ;
; 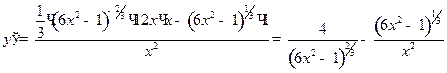 ;
;
2.14 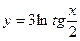 ;
; 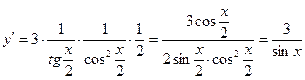 ;
;
2.15 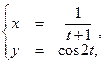 применим формулу
применим формулу 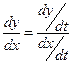 ;
;
вычислим 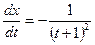 ;
; 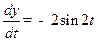 ;
; 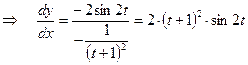 ;
;
2.16 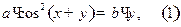
продифференцируем по 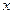 рав-во (1):
рав-во (1): 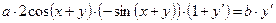 ;
; 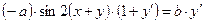 ;
; 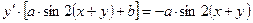 ;
; 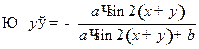 ;
;
2.17 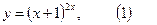
прологарифмируем рав-во (1): 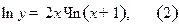
продифференцируем по 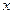 рав-во (2):
рав-во (2): 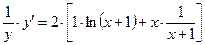 ;
;
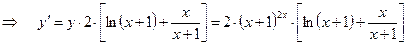 .
.
Задача 3 (смотри рис. 3)
Написать уравнения касательной и нормали к кривой 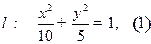 в точке
в точке 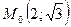 .
.
Сделать чертёж.
1) уравнение касательной 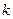 к кривой
к кривой 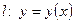 в точке
в точке 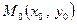 имеет вид:
имеет вид:
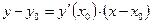 ; найдём
; найдём 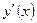 , для чего продифференцируем по
, для чего продифференцируем по 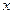 рав-во (1):
рав-во (1):
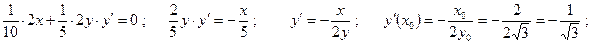
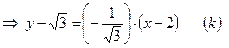 ;
;
2) уравнение нормали 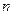 к кривой
к кривой 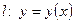 в точке
в точке 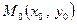 имеет вид:
имеет вид:
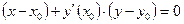 ; т. е.
; т. е. 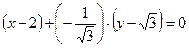 .
.
Задача 4
Составить уравнение касательной 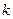 к кривой
к кривой 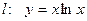 , зная, что эта касательная параллельна прямой
, зная, что эта касательная параллельна прямой
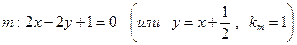 .
.
Пусть искомая касательная 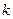 проходит через точку
проходит через точку 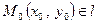 , тогда её уравнение имеет вид:
, тогда её уравнение имеет вид:
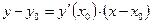 ; рассм.
; рассм. 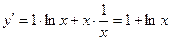 ;
; 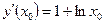 ; по условию задачи
; по условию задачи 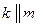 , след.,
, след., 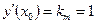 , т.е.
, т.е. 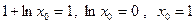 ;
;
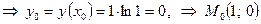 ;
; 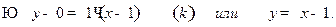
 2015-07-14
2015-07-14 483
483







